In this section we discuss the calculation of energy depositon to secondary particles for discrete two-body reactions. Suppose that particles 1 and 2 interact to form paricles x and y. Let mj denote the mass of particle j for j = 1, 2, x, and y, and let vj be its velocity in the laboratory frame. Then the kinetic of particle j in the laboratory frame is
The kinetic energies Ex and Ey of the particles x and y
depend on the angles at which they are ejected. The endep code
calculates the average values of Ex and Ey based on the
probability-density data for the angles (
![]() = 1 data).
Because this data is given in terms of the center-of-mass frame, we
have to make a transformation to laboratory coordinates before we
compute the average. The arguments given here are based on Newtonian
mechanics, so it is assumed that we are dealing with particles that
are not too energetic. We shall concentrate our attention on Ex
since by a choice of the labels x and y, this represents the
kinetic energy of either secondary particle.
= 1 data).
Because this data is given in terms of the center-of-mass frame, we
have to make a transformation to laboratory coordinates before we
compute the average. The arguments given here are based on Newtonian
mechanics, so it is assumed that we are dealing with particles that
are not too energetic. We shall concentrate our attention on Ex
since by a choice of the labels x and y, this represents the
kinetic energy of either secondary particle.
The following derivation of a formula for Ex in terms of E1 and Q is based on the reference [1, pp. 91-94]. The plan of attack is to transform to center-of-mass coordinates and work out the kinematics there, and then transform back to the laboratory frame. We use primes to denote quantities in center-of-mass coordinates. Thus, if V0 denotes the velocity of the center of mass,
then v1' = v1 - V0, etc. It follows from conservation of momentum thatLet us now consider the consequences of energy conservation in the center-of-mass system. It follows from the definition (3) of V0 that
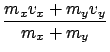 - V0
- V0
We now perform some algebraic manipulations, using (4)
and (6) to derive from (7) an equation
for Ex' in terms of E1. We begin by expressing all of the
kinetic energies in terms of squares of velocity differences,
| = |
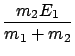 + Q =
+ Q =
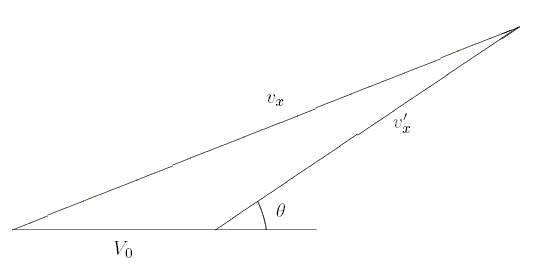
Figure 1: The relationship between velocities.
In order to transform (8) into the laboratory
frame, we need a relation between the velocities vx and vx'
depending on the collision angle ![]() in center-of-mass coordinates. In order to do this, we use the
fact that vx is the vector sum of vx' and
the velocity V0 of the center of mass. See Fig. 1. With
the notation that | V0| is the length of V0,
we find that
in center-of-mass coordinates. In order to do this, we use the
fact that vx is the vector sum of vx' and
the velocity V0 of the center of mass. See Fig. 1. With
the notation that | V0| is the length of V0,
we find that
The library data for the angular distribution (
![]() = 1
data) is given as the probability density
p(E1,
= 1
data) is given as the probability density
p(E1,![]() ) with respect
to the center-of-mass collision cosine
) with respect
to the center-of-mass collision cosine