We use a finite differencing method where the upper atomic population, n(x, t), is defined at the zone center, and for any time step, n(x, t) is constant within each zone.
We have tried two basic zoning schemes: equally spaced zones and spacing based on a geometric
progression starting from the surface, where the thickness of the surface zone was
close to one optical depth at line center. Figure 1 shows the
whole problem divided into 7 zones where a is the smallest zone, b is the length of the
slab, and 
is a multiplicative factor. Only the solid lines are to be considered; the dashed lines lines show a subzone scheme
that will be discussed later. We have found that this geometric spacing is
essential to accommodate the boundary layer: a rapid change of the atomic population with depth
near the surface and a rapid development of the spectrum of photons
leaving the surface. The SIMC method was more sensitive to zoning than the IMC method due to
the portion of the absorption that is transmuted into effective
scattering in IMC, but the same issues prevail in the limit of small time step size in IMC.
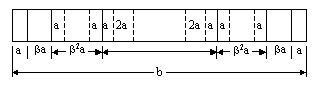
Figure 1: Geometric Zone and Subzone Construction
When the problem of interest involves high opacity, little transport occurs at line center. The emission profile is strongly peaked at line center but so is the absorption profile. As a result the more rarely produced frequencies (far from line center) travel further and account for much of the transport. This property of line transport (strongly emitted frequencies are also strongly absorbed) makes optically thick problems quite sensitive to zoning and importance sampling schemes. Straightforward Monte Carlo sampling of the emission profile, only to have these photons absorbed, produces results with excessive noise.