

Next: Continuum two-body reactions
Up: Discrete two-body reactions
Previous: Discrete two-body reactions
At low incident energies the angular distribution of secondary
particles is isotropic (with
p(E1,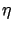 ) = 1/2), so that the
integral in (11) vanishes, and we have
) = 1/2), so that the
integral in (11) vanishes, and we have
For endothermic reactions (Q < 0) and for E1 near the threshold,
the arithmetic on the right-hand side of this equation may lead to the
subtraction of nearly equal numbers. In this circumstance we
therefore modify the calculation of
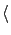 Ex
Ex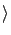 as follows.
as follows.
We begin by computing the threshold, which occurs when the secondary
particles have zero energy in the center-of-mass system. Thus, we set
Ex' = 0 and Ey' = 0 in (7) to get that the
threshold is when
E1' + E2' = - Q.
In terms of laboratory coordinates with a stationary target (v2 = 0), this equation takes the form
E1 -
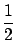
(
m1 +
m2)
V02 = -
Q.
We may now use (3) to write the velocity V0 of the center
of mass in terms of v1 to get that the threshold occurs when the
incident energy E1 is equal to
Ethreshold with
Ethreshold given by
In laboratory coordinates at threshold the secondary particles are
both moving at the velocity of the center of mass. The energy Ex
is therefore equal to
Ex =
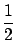 mxV02
mxV02.
By (3) this is equal to
Ex =
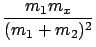 E1
E1,
and at the threshold
E1 = Ethreshold we find
from (13) that
Ex = - 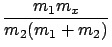 Q. Q.
|
(14) |
On the basis of these ideas, for an endothernmic reaction when the
incident particle is near threshold and the angular distribution is
isotropic, we calculate
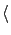 Ex
Ex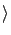 by using the formula
by using the formula
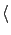 Ex Ex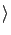 = ( = (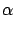 + + 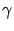 )(E1 - Ethreshold) - )(E1 - Ethreshold) - 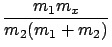 Q. Q.
|
(15) |
It is easy to show that the two equations, (15)
and (12), are mathematically equivalent. From the point
of view of computer arithmetic, however, (15) is
much more reliable.


Next: Continuum two-body reactions Up: Discrete two-body reactions Previous: Discrete two-body reactions
![]() ) = 1/2), so that the
integral in (11) vanishes, and we have
) = 1/2), so that the
integral in (11) vanishes, and we have
![]() Ex
Ex![]() by using the formula
by using the formula