- Atomic mass:
The mass of the target in atomic mass units (AMU). Historically,
this was called weight, hence the accessing routines are call ndfatw and ndfcatw
for ATomic Weight (atw).
- lMax:
The maximum Legendre order that data is calculated to and stored in the ndfy
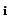 file.
This is only relevant for the transfer matrix when the incident particle
and outgoing particle are the same (i.e., yi = yo) and for the
transport correcting cross-sections. (When yi
file.
This is only relevant for the transfer matrix when the incident particle
and outgoing particle are the same (i.e., yi = yo) and for the
transport correcting cross-sections. (When yi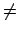 yo the outgoing particle
distribution is assumed to be isotropic; hence, only the l = 0 transfer matrix is stored).
See routines ndfmxorder, ndfcmxorder,
ndfmxorder_tc and ndfcmxorder_tc.
yo the outgoing particle
distribution is assumed to be isotropic; hence, only the l = 0 transfer matrix is stored).
See routines ndfmxorder, ndfcmxorder,
ndfmxorder_tc and ndfcmxorder_tc.
- Total cross-section:
The total cross-section is the sum of all the reaction cross-sections described in
item Reaction specific information below and has units of barn.
The access routines for this data are ndftotal, ndfsig,
ndfctotal and ndfcsig.
- Transport correcting cross-section:
Deterministic transport codes that use a Legendre expansion truncate the expansion due to
resource limitations. A truncation at order lT requires a correction from the next order
lT + 1. This correction is called the transport correcting cross-section in this document
and is label tcl in Table 3 with l = lT + 1.
Four transport correcting cross-section methods are supported by the ndf accessing routines.
Table 3 describes the four methods.
The default method is Pendlebury/Underhill.
Each transport correcting cross-section can be calculated for Legendre order 1 to lMaxtc where
lMaxtc is given in column 3 of Table 3.
The LLNL exact method has two caveats; (1) the lMax + 1 exact correction is really
the LLNL approximate method, (2) if the ith group total cross-section is less than
the exact tcl(i) then the exact tcl(i) is replaced by the approximate tcl(i).
Table 3:
List of the four transport correcting algorithm options available through the ndf access routines.
TMl is the lth Legendre order interaction transfer matrix (see item Transfer matrices),
fl(E) is the lth Legendre order flux and N3 is the lesser of i + 3 and ng.
lMaxtc is the highest Legendre order available for the specified algorithm.
| Code |
Name |
lMaxtc |
tcl(i) (for i = 1 to ng) |
| 0 |
None |
lMax + 1 |
0 |
| 1 |
Pendlebury/Underhill |
lMax |
TMl(i, i) |
| 2 |
LLNL (exact) |
lMax |
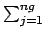 fl(j) TMl(i, j)/fl(i) fl(j) TMl(i, j)/fl(i) |
| |
LLNL (approximate) |
lMax + 1 |
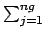 TMl(j, i) TMl(j, i) |
| 3 |
Ferguson |
lMax |
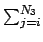 TMl(j, i) TMl(j, i) |
|
See routines ndfsig, ndftrcorr, ndfcorrec,
ndfncorrec, ndfcsig, ndfctrcorr, ndfccorrec and ndfcncorrec.
This data has units of barn.
- Reaction specific information:
Each target contains a list of all reactions included in its processing
as well as cross-section and particles produced (including
non-transportable particles) for each reaction. A reaction is identified by a unique
combination of C, S, Q, X1, X2, X3, and Q
eff-values. The C-value
identifies the type of reaction (e.g., C = 10 identifies the reaction as elastic scattering,
C = 11 identifies the reaction as inelastic scattering and C = 15 identifies the reaction as fission).
Some reaction types are sub-divided as given by the S-, X1-, X2-, and X3-values.
As example, for many targets the C = 11, inelastic scattering, reaction is sub-divided into
several level excitations (S = 1, X1 = level excitation MeV) and the rest (S = 0). The Q-value
is the mass difference of the reaction. Q
eff is the threshold-energy
for the reaction, and is typically, but not always, Q
calculated - X1.
Q
calculated is calculated during the processing stage from a table of masses, while Q
is taken from input data files that may contain slightly different masses;
whence Q
eff is close but not always equal to
Q - X1. All energy values have units of MeV.
The following two examples illustrate the type of reactions found in a ndfy file.
(Note, sometimes there is a
difference between the actual particles produced and those found in a ndfy
file.
(Note, sometimes there is a
difference between the actual particles produced and those found in a ndfy file.
During the processing of a ndfy
file.
During the processing of a ndfy file, the particles produced
(i.e., particles occurring on the right hand side of the
file, the particles produced
(i.e., particles occurring on the right hand side of the
 in
Tables 4 and 6)
are determined. If a product particle is not in the list of
targets in the ndfy
in
Tables 4 and 6)
are determined. If a product particle is not in the list of
targets in the ndfy file
then the processing code substitutes for it a nearby target that is in the ndfy
file
then the processing code substitutes for it a nearby target that is in the ndfy file.)
Tables 4 and 5 are an example of a neutron
incident on a 9Be target. This ndf1 file does not contain the targets 9Li, 8Li
and 6He, so they were replaced by the targets 7Li, 7Li and
file.)
Tables 4 and 5 are an example of a neutron
incident on a 9Be target. This ndf1 file does not contain the targets 9Li, 8Li
and 6He, so they were replaced by the targets 7Li, 7Li and  respectively.
The Q-values are calculated with the actual product particles and not the substituted ones.
respectively.
The Q-values are calculated with the actual product particles and not the substituted ones.
Table:
Example of the list of reactions for 9Be in a ndf1 file. The
 indicates lines that
are a duplicate of the line above them except that the product particle
substituted by the processing code is listed instead the actual product particle.
indicates lines that
are a duplicate of the line above them except that the product particle
substituted by the processing code is listed instead the actual product particle.
n + 9Be
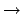 n + 9Be n + 9Be |
! C = 10, Elastic scattering |
n + 9Be
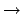 n + n + n + n +  + +  |
! C = 12, (n,2n) |
n + 9Be
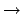 p + 9Li p + 9Li |
! C = 40, (n,p) |
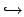 n + 9Be
n + 9Be
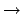 p + 7Li p + 7Li |
! 9Li replaced with 7Li |
n + 9Be
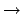 d + 8Li d + 8Li |
! C = 41, (n,d) |
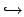 n + 9Be
n + 9Be
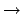 d + 7Li d + 7Li |
! 8Li replaced with 7Li |
n + 9Be
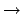 t + 7Li t + 7Li |
! C = 42, (n,t) |
n + 9Be
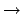  + 6He + 6He |
! C = 45, (n, ) ) |
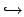 n + 9Be
n + 9Be
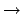  + +  |
! 6He replaced with  |
n + 9Be
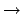 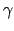 + 10Be + 10Be |
! C = 46, Capture |
|
Table 5:
Actual reaction data for the reactions in Table 4 as stored
in a ndf1 file.
| C |
S |
Q |
X1 |
X2 |
X3 |
Q
eff |
| 10 |
0 |
0. |
0. |
0. |
0. |
0. |
| 12 |
0 |
-1.5728 |
0. |
0. |
0. |
-1.5728 |
| 40 |
1 |
-12.83 |
0. |
0. |
0. |
-12.824 |
| 41 |
1 |
-14.66 |
0. |
0. |
0. |
-14.664 |
| 42 |
1 |
-10.44 |
0. |
0. |
0. |
-10.439 |
| 42 |
1 |
-10.44 |
0.478 |
0. |
0. |
-10.917 |
| 45 |
1 |
-0.6 |
0. |
0. |
0. |
-0.60175 |
| 46 |
0 |
6.82 |
0. |
0. |
0. |
6.82 |
|
Tables 6 and 7 are an example of a neutron
incident on a 10B target. Multiple C = 11 entries are present; four with S = 1 for the
excitation levels 0.717, 1.74, 2.154 and 3.59 MeV and one with S = 0 for the rest of the
inelastic reaction cross-section data.
Table 6:
Example of the list of reaction for 10B in a ndf1 file.
n + 10B
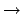 n + 10B n + 10B |
! C = 10, Elastic scattering |
n + 10B
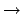 n' + 10B n' + 10B |
! C = 11, Inelastic scattering |
n + 10B
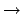 n + d + n + d +  + +  |
! C = 23, (n,n d  ) ) |
n + 10B
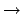 n + n + p + n + n + p +  + +  |
! C = 31, (n,2n p  ) ) |
n + 10B
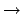 t + t +  + +  |
! C = 43, (n,t  ) ) |
n + 10B
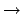  + 7Li + 7Li |
! C = 45, (n, ) ) |
n + 10B
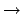 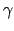 + 11B + 11B |
! C = 46, Capture |
|
Table 7:
Actual reaction data for the reactions in Table 6 as stored
in a ndf1 file.
| C |
S |
Q |
X1 |
X2 |
X3 |
Q
eff |
| 10 |
0 |
0. |
0. |
0. |
0. |
0. |
| 11 |
0 |
0. |
0. |
0. |
0. |
0. |
| 11 |
1 |
0. |
0.717 |
0. |
0. |
-0.717 |
| 11 |
1 |
0. |
1.74 |
0. |
0. |
-1.74 |
| 11 |
1 |
0. |
2.154 |
0. |
0. |
-2.154 |
| 11 |
1 |
0. |
3.59 |
0. |
0. |
-3.59 |
| 23 |
0 |
-6.02 |
0. |
0. |
0. |
-6.02 |
| 31 |
0 |
-8.158 |
0. |
0. |
0. |
-6.02 |
| 43 |
0 |
0.33 |
0. |
0. |
0. |
0.33 |
| 45 |
0 |
2.8 |
0. |
0. |
0. |
2.8 |
| 46 |
0 |
11.45 |
0. |
0. |
0. |
11.45 |
|
The access routines allow one to obtain information about the number of reactions,
the list of C-values, the summed cross-section and Q-value for a reaction type,
and the particles produced for a specific reaction as described below.
- Number of reactions:
The number of reactions for a specific target is obtained by calling
ndfnreact or ndfcnreact.
For Tables 5 and 7 the number of
reactions are 8 and 11 respectively.
Also see routines ndfreact, ndfnrxs, ndfrxs, ndfrxslist, ndfrxslevel,
ndfcreact, ndfcnrxs, ndfcrxs, ndfcrxslist and ndfcrxslevel.
- Reaction cross-section:
Reaction specific, for a specified C-value, cross-section data
are obtained by calling ndfrxs or ndfcrxs.
Also see routines ndfnrxs, ndfrxslist, ndfrxslevel, ndfcnrxs, ndfcrxslist
and ndfcrxslevel. This data has units of barn.
- Reaction particles produced:
The particles produced for a specified Reaction, C-value, are obtained by calling ndfprod or ndfcprod.
As example, for the C = 40 reaction for the data in Table 4, ndfnprod
would return 2 and ndfprod would return the lists ZAList = { 2, 3007 } and MList = { 1, 1 }
since two particles are produced (i.e., p and 7Li), each with multiplicity 1.
Also see routines ndfnprod, and ndfcnprod.
- Transportable particles produced, (i.e., yos):
Each target produces transportable particles. For example, the 9Be target of
Table 4 and the 10B target of Table 6 each
produce 6 transportable particles (n, p, d, t,
 and
and 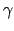 ).
The number of difference
transportable particle types produced is obtained by calling
ndfnyos or ndfcnyos. A list of transportable particle types produced
is obtained by calling ndfyos or ndfcyos. Also see routines
ndfnppyos, ndfppyos, ndfcnppyos, and ndfcppyos
which are similar but do not include the incident transportable particle in the number of
particles produced or the list.
).
The number of difference
transportable particle types produced is obtained by calling
ndfnyos or ndfcnyos. A list of transportable particle types produced
is obtained by calling ndfyos or ndfcyos. Also see routines
ndfnppyos, ndfppyos, ndfcnppyos, and ndfcppyos
which are similar but do not include the incident transportable particle in the number of
particles produced or the list.
- Transfer matrices:
The formulas for the transfer matrices will not be presented here; instead, see chapter VI
of reference [1] and reference [2]. In summary, three methods
can be used to calculate a transfer matrix, depending on whether particle number, energy or number/energy
of the outgoing particles is to be conserved during the processing (see item yo descriptor in
Section 5.1). Only the particle number conserving transfer matrix is outlined here.
The particle number conserving
transfer matrix for outgoing particle yo is defined as,
Here, h is the outgoing particle's group designation,
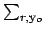 means to
sum only reactions that produce yo as an outgoing particle,
means to
sum only reactions that produce yo as an outgoing particle,
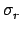 (E) and
Mr, yo(E) are the cross-section and multiplicity respectively
for the reaction (e.g., for the C = 13, (n,3n), reaction and yo = 1,
M13, 1(E) = 3) and
(E) and
Mr, yo(E) are the cross-section and multiplicity respectively
for the reaction (e.g., for the C = 13, (n,3n), reaction and yo = 1,
M13, 1(E) = 3) and
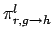 is the grouped, lth Legendre coefficient of the normalized probability
of the incident particle of energy E producing the required outgoing particle with
energy E' at angle
is the grouped, lth Legendre coefficient of the normalized probability
of the incident particle of energy E producing the required outgoing particle with
energy E' at angle 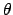 .
.
The transfer matrices are divided into two types. The first type is called the interaction
transfer matrix and is the transfer matrix when the incident transportable particle type is the
same as the outgoing transportable particle type (i.e., y
i 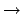 yo for yi = yo).
The interaction transfer matrix is calculated to Legendre order l = lMax + 1 during processing,
so that the lMax + 1 LLNL approximate transport correcting cross-sections can be calculated,
but is only stored to order
l = lMax in the ndfy
yo for yi = yo).
The interaction transfer matrix is calculated to Legendre order l = lMax + 1 during processing,
so that the lMax + 1 LLNL approximate transport correcting cross-sections can be calculated,
but is only stored to order
l = lMax in the ndfy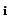 file. These matrices are accessed with routines ndfsig,
ndftransfer, ndfcsig and ndfctransfer.
The second type of transfer matrix is called the production transfer matrix. This matrix is the
transfer matrix when the incident transportable particle type is different than the
outgoing transportable particle type (i.e., y
i
file. These matrices are accessed with routines ndfsig,
ndftransfer, ndfcsig and ndfctransfer.
The second type of transfer matrix is called the production transfer matrix. This matrix is the
transfer matrix when the incident transportable particle type is different than the
outgoing transportable particle type (i.e., y
i 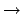 yo for yi
yo for yi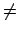 yo) and is only calculated
for Legendre order l = 0.
These matrices are accessed with routines ndfnppyos, ndfppyos, ndfpmat, ndfppmatrix,
ndfcnppyos, ndfcppyos, ndfcpmat and ndfcppmatrix.
This data has units of barn.
yo) and is only calculated
for Legendre order l = 0.
These matrices are accessed with routines ndfnppyos, ndfppyos, ndfpmat, ndfppmatrix,
ndfcnppyos, ndfcppyos, ndfcpmat and ndfcppmatrix.
This data has units of barn.
The multiplicity factor in Eq. 16
often leads to confusion with users of the ndf access routines as they assume that the
total cross-section must be greater than or equal to the l = 0 interaction transfer matrix integrated
over outgoing particle energy; since the sum is only over reactions that produce
a specific outgoing particle. To understand the confusion, consider
a simple problem with a neutron incident on target X that only has the two reactions C = 10 (n,n)
and C = 13 (n,3n).
Let both reactions' cross-sections be isotropic, independent of energy and 1 barn.
Thus, the l = 0 interaction transfer matrix integrated over
outgoing particle energy is 4 barns (1 x 1. barn + 3 x 1. barn) which is greater than
the total cross-section of 2 barns.
- Fission
<
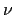
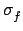 > g:
For neutrons produced by fission, C = 15, the multiplicity is dependent on energy and not an integer
(since it is an average multiplicity over many possible fission channels).
The average number of neutrons produced by fission
<
> g:
For neutrons produced by fission, C = 15, the multiplicity is dependent on energy and not an integer
(since it is an average multiplicity over many possible fission channels).
The average number of neutrons produced by fission
< 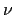
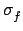 > g is stored for targets
that fission and is calculated as,
where
> g is stored for targets
that fission and is calculated as,
where
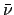 (E) is the number of neutrons produced by fission average over possible fission channels
and
(E) is the number of neutrons produced by fission average over possible fission channels
and 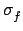 is the fission cross-section.
This data only occurs for neutron as incident particle (yi = 1) and when the neutron multiplicity
returned by ndfprod or ndfcprod is 0.
This data is accessed with routines ndffisx and ndfcfisx, and has units of barn.
is the fission cross-section.
This data only occurs for neutron as incident particle (yi = 1) and when the neutron multiplicity
returned by ndfprod or ndfcprod is 0.
This data is accessed with routines ndffisx and ndfcfisx, and has units of barn.
- Fission neutron transfer matrix:
For targets in a ndf1 file that have fission data the l = 0 fission transfer matrix is calculated.
It is calculated just like the l = 0 interaction transfer matrix except only the fission reaction
data is used. See routines ndffisx ndfifsp, ndffsp, ndfcfisx, ndfcifsp and ndfcfsp.
This data has units of barn.
- Energy conservation and energy data:
To conserve energy, particles that are not transported by a code have to have their energy deposited
locally. The amount of energy that must be deposited locally and how to obtain it from
a ndfy
 file is outlined below.
file is outlined below.
During the processing of a ndfy file, the average kinetic energy of an incident particle in group g
is calculated as,
file, the average kinetic energy of an incident particle in group g
is calculated as,
Here,
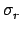 (E) is the cross-section for a given reaction and
(E) is the cross-section for a given reaction and 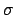 (E) is the total cross-section.
(E) is the total cross-section.
The average energy due to the mass differences between the before and after reaction particles,
called the production energy (see item ep below), is calculated as,
where Qr is the sum of the incident particle's and target's masses minus the sum of all outgoing
particles' masses (this includes non-transportable particles).
The sum of Eqs. 18 and 19 is the total available energy
(see item emax below),
< E 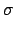 > g, Available = < E > g, Available = < E 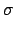 > g + < Q > g + < Q 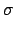 > g . > g .
|
(20) |
During the processing the average energy deposited to a transportable outgoing particles
(see item ed(yo) below) is calculated as,
Here
E'r, yo is the average energy deposited to a transportable particle of type yo for reaction r. The
amount of energy to be locally deposited is calculated as the total available energy, Eq 20,
minus the energy deposited to all transportable outgoing particles that are being transported.
- emax:
This is the total available energy (Eq. 20) and has units of MeV-barn.
This data is accessed using ndfemax or ndfcemax.
- ep:
This is the production energy (Eq. 19) and has units of MeV-barn.
This data is accessed using ndfep or ndfcep.
- ed(yo):
This is the average energy deposited to transportable outgoing particle yo (Eq. 21)
and has units of MeV-barn.
This data is accessed using ndfsig or ndfcsig when (yo = yi) and is
accessed using ndfpmat or ndfcpmat when (yo
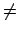 yi). Also see routines
ndfed, ndfnyos, ndfyos, ndfced, ndfcnyos and ndfcyos.
yi). Also see routines
ndfed, ndfnyos, ndfyos, ndfced, ndfcnyos and ndfcyos.
![]() file.
(Note, sometimes there is a
difference between the actual particles produced and those found in a ndfy
file.
(Note, sometimes there is a
difference between the actual particles produced and those found in a ndfy![]() file.
During the processing of a ndfy
file.
During the processing of a ndfy![]() file, the particles produced
(i.e., particles occurring on the right hand side of the
file, the particles produced
(i.e., particles occurring on the right hand side of the
![]() in
Tables 4 and 6)
are determined. If a product particle is not in the list of
targets in the ndfy
in
Tables 4 and 6)
are determined. If a product particle is not in the list of
targets in the ndfy![]() file
then the processing code substitutes for it a nearby target that is in the ndfy
file
then the processing code substitutes for it a nearby target that is in the ndfy![]() file.)
Tables 4 and 5 are an example of a neutron
incident on a 9Be target. This ndf1 file does not contain the targets 9Li, 8Li
and 6He, so they were replaced by the targets 7Li, 7Li and
file.)
Tables 4 and 5 are an example of a neutron
incident on a 9Be target. This ndf1 file does not contain the targets 9Li, 8Li
and 6He, so they were replaced by the targets 7Li, 7Li and ![]() respectively.
The Q-values are calculated with the actual product particles and not the substituted ones.
respectively.
The Q-values are calculated with the actual product particles and not the substituted ones.
 and
and 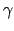 ).
The number of difference
transportable particle types produced is obtained by calling
ndfnyos or ndfcnyos. A list of transportable particle types produced
is obtained by calling ndfyos or ndfcyos. Also see routines
ndfnppyos, ndfppyos, ndfcnppyos, and ndfcppyos
which are similar but do not include the incident transportable particle in the number of
particles produced or the list.
).
The number of difference
transportable particle types produced is obtained by calling
ndfnyos or ndfcnyos. A list of transportable particle types produced
is obtained by calling ndfyos or ndfcyos. Also see routines
ndfnppyos, ndfppyos, ndfcnppyos, and ndfcppyos
which are similar but do not include the incident transportable particle in the number of
particles produced or the list.
![]() yo for yi = yo).
The interaction transfer matrix is calculated to Legendre order l = lMax + 1 during processing,
so that the lMax + 1 LLNL approximate transport correcting cross-sections can be calculated,
but is only stored to order
l = lMax in the ndfy
yo for yi = yo).
The interaction transfer matrix is calculated to Legendre order l = lMax + 1 during processing,
so that the lMax + 1 LLNL approximate transport correcting cross-sections can be calculated,
but is only stored to order
l = lMax in the ndfy![]() file. These matrices are accessed with routines ndfsig,
ndftransfer, ndfcsig and ndfctransfer.
The second type of transfer matrix is called the production transfer matrix. This matrix is the
transfer matrix when the incident transportable particle type is different than the
outgoing transportable particle type (i.e., y
i
file. These matrices are accessed with routines ndfsig,
ndftransfer, ndfcsig and ndfctransfer.
The second type of transfer matrix is called the production transfer matrix. This matrix is the
transfer matrix when the incident transportable particle type is different than the
outgoing transportable particle type (i.e., y
i ![]() yo for yi
yo for yi![]() yo) and is only calculated
for Legendre order l = 0.
These matrices are accessed with routines ndfnppyos, ndfppyos, ndfpmat, ndfppmatrix,
ndfcnppyos, ndfcppyos, ndfcpmat and ndfcppmatrix.
This data has units of barn.
yo) and is only calculated
for Legendre order l = 0.
These matrices are accessed with routines ndfnppyos, ndfppyos, ndfpmat, ndfppmatrix,
ndfcnppyos, ndfcppyos, ndfcpmat and ndfcppmatrix.
This data has units of barn.
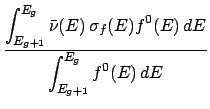
![]() file, the average kinetic energy of an incident particle in group g
is calculated as,
file, the average kinetic energy of an incident particle in group g
is calculated as,
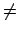 yi). Also see routines
ndfed, ndfnyos, ndfyos, ndfced, ndfcnyos and ndfcyos.
yi). Also see routines
ndfed, ndfnyos, ndfyos, ndfced, ndfcnyos and ndfcyos.
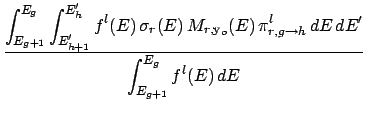
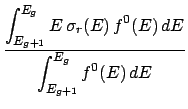
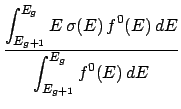 .
.
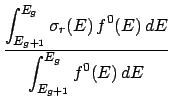
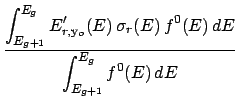
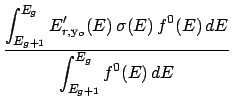 .
.