2⁶² -2¹⁶ + 1 Modulus Linear Congruential Generator

A second prime modulus generator that addresses the pattern appearing for Mersenne primes is provided by the prime modulus 2⁶² -2¹⁶ + 1. This is provided by the recurrence relation:

x[n] = a x[n - 1]   (modp) (8)

Where the multiplier, a = 3355703948966806692, is hardwired into the algorithm and p, the prime modulus, is 2⁶² -2¹⁶ + 1. The multiplier was again chosen to obtain maximal period of the generator, 2⁶² -2¹⁶ 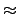$\approx$ 4.6 x 10¹⁸. The interface routines for this generator are declared as: Rng_Type RngP62_16Seed( Rng_UInt32 i, Rng_UInt32 j );

Rng_Type RngP62_16Spawn( Rng_Type *x );

int iRngP62_16( Rng_Type *x );

double dRngP62_16( Rng_Type *x );

float fRngP62_16( Rng_Type *x );

This random number generator suffers from no patterns that we are aware of and we are currently evaluating its quality using statistical tests.