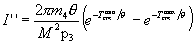UCRL-ID-144510
The TDF System for Thermonuclear Plasma Reaction Rates, Mean Energies and Two-Body Final State Particle Spectra
Stephen I. Warshaw
July 11, 2001
N Division
Physics and Advanced Technologies Directorate
Lawrence Livermore National Laboratory
Livermore, CA 94551
Table of Contents
2. The Maxwellian-averaged
thermonuclear reaction rate 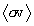
3. Maxwellian-averaged mean energies and cosines for two-body final state reactions
5. Maxwellian-averaged two-body final state reaction particle spectra
6. Digression on two-body final state spectrum moments
7. Data,
algorithmic bases and results of  calculations
calculations
8. Algorithmic
bases and results for  ,
,
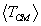 and
and 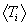
9. Algorithmic basis of the final state spectral probability distributions
10. The Thermonuclear Data File (TDF) generator
11. Structure and content of the TDF
12. The TDFLIB subroutine library
Appendix A. Example TDF format
Appendix B. Erratum in Williams' original paper
Appendix C. Evaluation of a d function integral over finite limits
The rate of thermonuclear reactions in hot plasmas as a function of local plasma temperature determines the way in which thermonuclear ignition and burning proceeds in the plasma. The conventional model approach to calculating these rates is to assume that the reacting nuclei in the plasma are in Maxwellian equilibrium at some well-defined plasma temperature, over which the statistical average of the reaction rate quantity sv is calculated, where s is the cross-section for the reaction to proceed at the relative velocity v between the reacting particles. This approach is well-understood and is the basis for much nuclear fusion and astrophysical nuclear reaction rate data. (See, e.g., Chiu 1968, Clayton 1968)
The Thermonuclear Data File (TDF) system developed at the Lawrence Livermore National Laboratory (Warshaw 1991), which is the topic of this report, contains data on the Maxwellian-averaged thermonuclear reaction rates for various light nuclear reactions and the correspondingly Maxwellian-averaged energy spectra of the particles in the final state of those reactions as well. This spectral information closely models the output particle and energy distributions in a burning plasma, and therefore leads to more accurate computational treatments of thermonuclear burn, output particle energy deposition and diagnostics, in various contexts. In this report we review and derive the theoretical basis for calculating Maxwellian-averaged thermonuclear reaction rates, mean particle energies, and output particle spectral energy distributions for these reactions in the TDF system. The treatment of the kinematics is non-relativistic. The current version of the TDF system provides exit particle energy spectrum distributions for two-body final state reactions only. In a future report we will discuss and describe how output particle energy spectra for three- and four-body final states can be developed for the TDF system.
We also include in this report a description of the algorithmic implementation of the TDF system, which is in two parts: the code which generates the data file itself from the nuclear reaction cross-sections, and the lookup utilities (bundled in a Fortran 77 subroutine library) which are used to retrieve the appropriate thermo-nuclear data from the file on demand. Unique approaches to generating, retrieving and looking up the data that were developed will be described in some detail. These developments resulted in an unusually compact data file which can be quickly generated, and from which an enormous amount of thermonuclear reaction rate, output particle energy and particle energy spectrum data can be rapidly retrieved. It is this compactness, speed and relative platform independence that distinguishes the LLNL TDF system from others.
2. The Maxwellian-averaged thermonuclear reaction rate 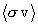
Consider a plasma containing a mixture of two nuclear species which react to produce other particles and nuclei. We quantify the rate of thermonuclear reaction by first considering a "local" microscopic model in which one of the nuclear species is at rest, and the other is traveling toward the stationary nuclei in a beam moving at velocity v, as shown schematically in Figure 1.
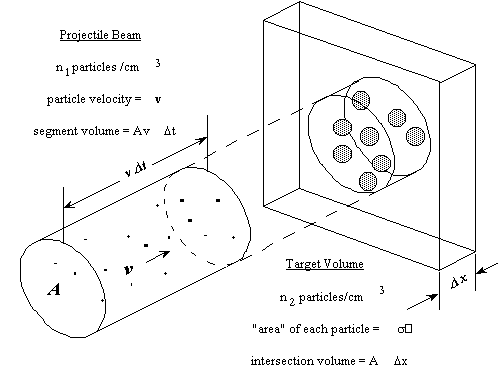
Figure 1. Particle-beam particle-target geometry
With the geometric notions shown in the figure, the number of particles in the beam segment is
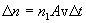 ,
,
where A is the area of the beam cross-section (and therefore the area of the particle interaction volume). The total area presented by the target particles within the particle interaction volume to the particles in the beam is
 .
.
Thus the fraction of the particle beam that is intercepted by the target particles is
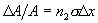 ,
,
and the total number of beam particle - target particle interactions is therefore
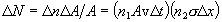 .
.
Since the interaction volume is ADx and the interaction time is Dt, we then have that the number of interactions per unit volume per unit time is
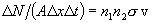 .
.
This quantity is considered to be the instantaneous local reaction rate density for the binary plasma in question when it is understood that v is the scalar relative velocity
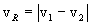
between the nuclei of the different species, the binary interaction cross-section s is strictly a function of vR, and the particle densities n1 and n2 are understood to be locally constant and uniform.
In a plasma the velocities v1 and v2 of two interacting component species of particle are distributed in magnitude and direction, so that the number of particles per unit volume of species type 1 having a mean velocity v1 within the differential cell d3v1 = dv1xdv1ydv1z in velocity space is
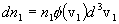 ,
,
and the number of particles per unit volume of species type 2, similarly, is
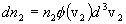 ,
,
where f(vi) is symbolic for the normalized distribution function for particle species i in the plasma. Then the total reaction rate density for the interacting species in the plasma is the integral of the local reaction rate density over all possible particle pair combinations and vector relative velocities, as follows:
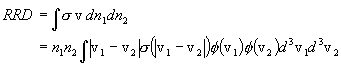
Note that this is an integral over a joint distribution f(v1)f(v2). Since the functions f(vi) are assumed normalized, that is,
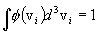
this quantity is also the statistical average of n1n2sv over the joint distribution, and may therefore be written as
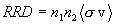 .
.
In the case where both reacting particles are identical (as in the d(d,n)3He reaction, for example), the RRD needs to be calculated differently, because during the double integration over dn1dn2 the same particle population is integrated over twice. This means that each reacting particle pair is counted twice, and the RRD in this case is double what it should be. The correct formulation of the RRD in the general case is therefore as follows:
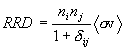
where i and j denote the reacting particle species, and dij is the Kronecker delta, which is equal to 1 when i = j and 0 otherwise. (This multiplying factor issue is discussed more thoroughly by Clayton (1968)).
Because the particle densities ni
and nj are particular
to a given plasma configuration and so may themselves be distributed in time
and space, we have formulated the TDF system to provide only the "bare"
statistical average 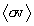 . It therefore does not include the
pair count multiplier ninj/(1
+ dij). In this report we treat only the
statistical average
. It therefore does not include the
pair count multiplier ninj/(1
+ dij). In this report we treat only the
statistical average 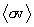 and ignore the multiplier, as well.
and ignore the multiplier, as well.
In our modeling we assume the reacting particle species each have an isotropic Maxwellian distribution at a common kinetic temperature q = kT. Then the particle distribution functions for each species also depend on particle mass and plasma temperature, and have the well-known form
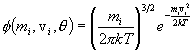
where mi is the particle mass, vi2 is the square of the magnitude of the vector velocity vi, and i = 1 or 2 identifies the particle species. These functions are normalized. Using these functions, the statistically averaged reaction rate density for the two species in thermal equilibrium at a plasma temperature q = kT is given by the following expression:
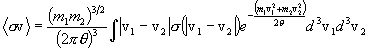 .
.
This is the formal development of the Maxwellian-averaged thermonuclear reaction
rate 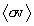 in
integral form. It is clear that
in
integral form. It is clear that 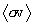 is
a function of q. (Brysk (1973) worked
out
is
a function of q. (Brysk (1973) worked
out 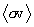 for the case where the two reacting components
each have a Maxwellian distribution but at different temperatures.)
for the case where the two reacting components
each have a Maxwellian distribution but at different temperatures.)
This integral can be put in a simpler form by changing the velocity variables from v1 and v2 to the relative velocity
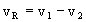
and the center-of-mass velocity
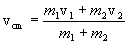 .
.
The total kinetic energy then transforms as
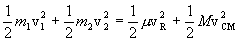
where M = m1 +
m2 is the total
mass of the system andm = m1m2/M
is its reduced mass. The term 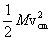 is denoted by Tcm and is the kinetic energy of the center
of mass of the particle system. The term
is denoted by Tcm and is the kinetic energy of the center
of mass of the particle system. The term 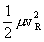 is denoted by TR and is the kinetic energy of relative
motion; it is equal to the sum of the kinetic energies of the two reacting
particles in their center-of-mass (cm) frame. It is also proportional to
the incident laboratory frame bombarding energy of one particle when the other
(the target) is at rest, since the relative velocity vR
is the same in all frames of reference.
is denoted by TR and is the kinetic energy of relative
motion; it is equal to the sum of the kinetic energies of the two reacting
particles in their center-of-mass (cm) frame. It is also proportional to
the incident laboratory frame bombarding energy of one particle when the other
(the target) is at rest, since the relative velocity vR
is the same in all frames of reference.
The Jacobian of this transformation is unity, so the differential
elements transform directly as d3v1d3v2 = d3vRd3vcm.
On applying this transformation to the integral for 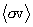 , we find that this integral separates into
two parts, as follows:
, we find that this integral separates into
two parts, as follows:
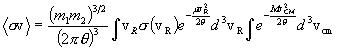 .
.
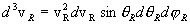
and
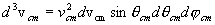 .
.
On the assumption of particle direction isotropy within the plasma, the integrations over the polar angles can be carried out immediately, to yield the result that
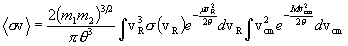 .
.
This may be further simplified by making one more variable substitution in
the form 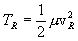 , and carrying out the integration over dvcm. Then we obtain the single integral
for
, and carrying out the integration over dvcm. Then we obtain the single integral
for 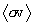 as
as
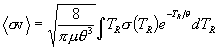 .
.
The integrand 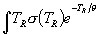 is sometimes called the Gamow distribution
function.
is sometimes called the Gamow distribution
function.
Note that the above reaction rate results hold for any initial pair of reacting nuclei whose total reaction cross-section is specified, and are independent of how many particles or additional channels result in the final state. Thus, if one of the final state particles breaks up into additional particles, or any exit nuclei are left in excited states, the total reaction rate is still the same. On the other hand, if the cross-section chosen is specific to a particular final state channel out of many channels for the same two initial reacting particles, then the reaction rate associated with this channel will necessarily be different.
We also note in passing that Slaughter (1983, 1985, 1986, 1989) describes Monte Carlo calculations of reaction rates and output particle spectra for other types of particle distributions in which the particle motions are not isotropic, and therefore non-Maxwellian. This occurs, for instance, when a directed beam of one species of particle with a narrow energy spread is incident on a quiescent plasma containing other species of particles.
3. Maxwellian-averaged mean energies and cosines for two-body final state reactions
The intrinsic properties of the thermonuclear reaction components during the plasma conditions are also of interest. These include the mean kinetic energies, directions and energy spectra of the incident and exit particles, which can be used to estimate, e.g., energy deposition or diagnostic particle outputs as thermonuclear burn proceeds (Slaughter 1989). In this section we develop the Maxwellian-averaged mean energies and direction cosines for the reacting and exit particles of two-body final state reactions. In the next section we develop model estimates for the mean energies of the exit particles of three-body final state reactions, specializing to the t(t,2n)a reaction. Corresponding exit particle energy spectra for two-body final state reactions are discussed in the section after that. Spectra for three-body final state reactions are more complex and will be treated in a separate report.
A two-body final state nuclear reaction taking place in a plasma is depicted schematically in Figure 2, where the two incident and two exit particles are labeled with the indices 1 through 4, and the corresponding masses, velocities and angles are appropriately labeled. We observe that the incident and exit vector pairs (v1,v2) and (v3,v4) each define planes containing the common vector vcm, which is the velocity of the center of mass of the interacting and exit particle pairs. We assume in our development that the nuclear reaction is such that the orientations of these two planes are not correlated by the interaction, and are therefore arbitrary. The incident vectors are therefore not coplanar with the exit vectors, in general.
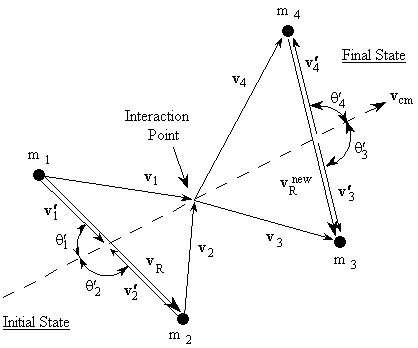
Figure 2. Two-body final state reaction kinematics
The kinetic energies of each particle are labeled in the plasma
(i.e. "lab") frame as 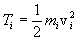 , while in the "center of mass"
(cm) frame they are written as
, while in the "center of mass"
(cm) frame they are written as 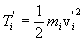 . The kinetic energies of the motion of
the center of mass and the relative motion of the incident particles are related
to these particle energies as follows:
. The kinetic energies of the motion of
the center of mass and the relative motion of the incident particles are related
to these particle energies as follows:
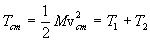
and
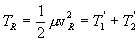 ,
,
where
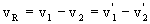 .
.
The kinetic energy associated with the relative motion of the exit particles is
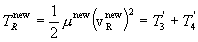
where
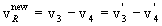
and
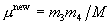 .
.
We assume that the quantities M (= m1 + m2 = m3 + m4), Tcmand vcm are the same before and after the interaction, within a very small error (of the order of Q/Mc2 where M is the total reaction particle mass), and that the relative velocities vR and vRnew are each independent of frame of reference.
We calculate Maxwellian-averaged mean properties of these reaction quantities by first expressing all energies in terms of TR and Tcm, since, as we will show, this facilitates developing the separable expressions for their statistical averaging. This transformation, however, has a much deeper significance apart from this convenient consequence, because it effectively separates the plasma-related phenomenology and the nuclear interaction. This is because in any interaction in the plasma, the center of mass motion vcm and the relative particle motion vR are independent of one another, i.e. uncorrelated. Thus the center of mass kinetics are determined solely by the plasma properties, and none of the nuclear interaction properties depend on any of the center of mass quantities — including the direction of vcm. And, s is a function of TR and not of Tcm. This is why — as we will show later — the statistical average of Tcm depends on q, that for TR depends on both q and s, and the angular correlations between relative and center of mass motion quantities average to zero.
We first express the initial particle velocities in terms of vR and vcm, as follows:
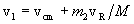
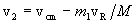 .
.
From this we see that v1¢ = m2vR/M and v2¢ = - m1vR/M. It is then a fairly straightforward procedure to use the previous definitions of the various kinetic energies to obtain the initial state energies and relations in terms of Tcm and TR:
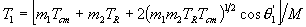
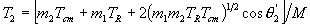
and
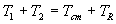 ,
,
where the qi¢ are the angles that v1¢ and v2¢(and therefore vR) make with vcm, as shown in Figure 2. In other words,
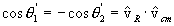
where the caret ( ˆ ) denotes the unit vector.
The final state particle energies and relations are correspondingly rendered, when it is understood that the reaction Q-value (the energy released by the reaction process) is included only in the final particle energy and velocities, and leaves the center of mass quantities Tcm, vcm and M unaffected with negligible error. This says that
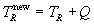
is the only essential difference; thus the relations for the final state can be copied directly from those of the initial state by appropriately relabeling the particle indices. We then have that
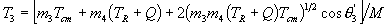
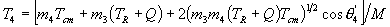
and
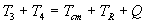 .
.
q3¢
and q4¢
are the angles that v3¢
and v4¢(and
therefore 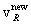 ) make with vcm, as shown in Figure 2, so that
) make with vcm, as shown in Figure 2, so that
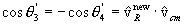 .
.
We can now address the statistical average of these reaction
energies and cosines over the plasma distribution, and this requires some
care. Basically, the only way to obtain the mean value of a reaction
quantity in a plasma is to calculate its average over a reaction probability
distribution, and the only distribution that qualifies is the reaction rate
function that determines 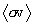 –
not just the Maxwellian distribution of the plasma. This function
is the integrand used to calculate
–
not just the Maxwellian distribution of the plasma. This function
is the integrand used to calculate 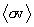 , or
, or
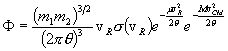 .
.
which is a joint probability distribution in d3vRd3vcm space. It is important to note that this function identifies, or selects, in a statistical sense, the distribution of that part of the particle population of the plasma that participates in the reaction, and only that part. It is also important to notice that this distribution identification holds for any and all final state configurations that result from the reaction, which is to say that it is independent of whatever values and directions the final state particle velocities do take. As we will show shortly, this concept is the key element that helps resolve anisotropic differential cross-section issues (Perkins, 1990 and 1991) that arise in calculating the Maxwellian-averaged reaction quantities for the final state.
Because F is not normalized to 1 (its integral is
equal to 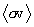 ), the statistical average of any quantity,
say f, over this reaction probability distribution, which we denote
by
), the statistical average of any quantity,
say f, over this reaction probability distribution, which we denote
by 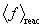 , is calculated by the classic ratio of two
integrals,
, is calculated by the classic ratio of two
integrals,
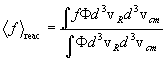
where the subscript "reac" on the angular brackets denotes the
statistical average over the reaction distribution F, and the angular brackets without a subscript
continue to denote the statistical average over the Maxwellian distribution.
Thus the denominator in the above is, of course, 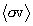 , while the numerator is (now obviously)
the Maxwellian average
, while the numerator is (now obviously)
the Maxwellian average 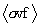 . We can write this more compactly as
. We can write this more compactly as
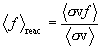 .
.
Notice that the exponents in the integrands are TR/q and Tcm/q, which is the reason for rewriting all kinematic quantities in terms of TR and Tcm. This means that if the quantity f is separable into functions of TR, Tcm (or vR, vcm) or the angular directions, then individual integrations over these arguments can proceed separately. As it turns out this will indeed be so for our needs.
We developed Ti
in terms of TR,
Tcm and the cosines given by 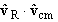 and
and 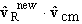 . It is a fairly easy matter to obtain the reaction
rate averages of these latter quantities, since their integrals are now separable.
The statistical reaction average for TR
reduces to a single integral much the same way as the statistical Maxwellian
average for sv worked out,
and the result is
. It is a fairly easy matter to obtain the reaction
rate averages of these latter quantities, since their integrals are now separable.
The statistical reaction average for TR
reduces to a single integral much the same way as the statistical Maxwellian
average for sv worked out,
and the result is
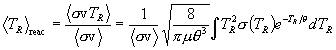
Here, too, numerical integration is required, in an equally simple form as
for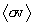 .
.
Zimmerman (2001) has pointed out that the slope of the 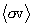 curve as a function of q
is related to
curve as a function of q
is related to 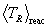 . This is immediately evident by
differentiation: one finds, by including the ∂ /∂q operation on the
. This is immediately evident by
differentiation: one finds, by including the ∂ /∂q operation on the 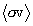 integrand, that
integrand, that
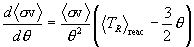 .
.
Thus 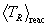 can be expressed in terms of
can be expressed in terms of 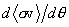 . The reaction statistical average for Tcm
easily reduces to its Maxwellian average:
. The reaction statistical average for Tcm
easily reduces to its Maxwellian average:
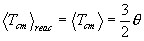 .
.
Finally, we consider the reaction averages of the particle direction
cosines, which contain some subtle issues. To calculate the reaction statistical
average of the cosine term 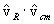 , we select the direction of vcm
as the z-axis for the polar coordinate system for vR. Then
, we select the direction of vcm
as the z-axis for the polar coordinate system for vR. Then
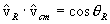
and the angular integral part (in the vR system) of the reaction average of this quantity vanishes:
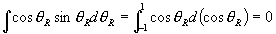 .
.
Thus
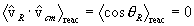 .
.
This reiterates our earlier observation that vR and vcm are uncorrelated. The reaction statistical average of the cross-terms in the expressions for T1 and T2 therefore vanish.
Next, we calculate the reaction statistical average of the post-reaction
cosine term 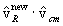 . However, the angular anisotropy in the
emission of final state products needs to be addressed, because the angular
distributions ds/dW of final
state particles in nuclear reactions are neither uniform nor constant. As
it turns out (Zimmerman 1990) this is of no consequence, because the angular
distribution is a function of the angle that
. However, the angular anisotropy in the
emission of final state products needs to be addressed, because the angular
distributions ds/dW of final
state particles in nuclear reactions are neither uniform nor constant. As
it turns out (Zimmerman 1990) this is of no consequence, because the angular
distribution is a function of the angle that 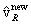 makes with the initial relative velocity
direction
makes with the initial relative velocity
direction 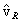 , and the direction cosine of
, and the direction cosine of 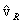 , as we showed earlier, has a reaction statistical
average of zero. We may put this in another, more graphical way. Suppose
one of the final state reaction particles was emitted preferentially at some
fixed angle a which
, as we showed earlier, has a reaction statistical
average of zero. We may put this in another, more graphical way. Suppose
one of the final state reaction particles was emitted preferentially at some
fixed angle a which 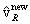 makes relative to the original interaction
particle direction of approach,
makes relative to the original interaction
particle direction of approach, 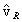 . The statistical average would then be
taken of the cosine of this direction relative to the direction of
. The statistical average would then be
taken of the cosine of this direction relative to the direction of 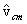 (which is the polar axis for the integration).
We are therefore in fact calculating the statistical reaction average of the
quantity
(which is the polar axis for the integration).
We are therefore in fact calculating the statistical reaction average of the
quantity
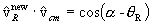 ,
,
and this, too, results in zero. Thus the reaction statistical average of the cross-terms in the expressions for T3 and T4 also vanish.
The reaction statistical average of the particle kinetic energies in the plasma are thus as follows:
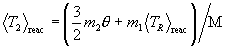
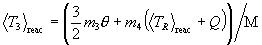
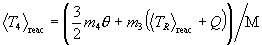 .
.
Energy conservation clearly still holds during reaction averaging:
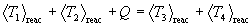
We emphasize again that the statistical averages which are labeled by the subscript "reac" are over only those particles that actually participate in the reaction, and not the entire plasma population. The above conservation law is thus so restricted. Perkins and Howerton (1988) obtain the same results but with a priori initial assumptions of average energy conservation and isotropy of reaction angular distributions. Our treatment does not require these assumptions.
4. Exit particle energies in the t(t,2n)a reaction: a foray into three-body final state energy averaging
The Maxwellian-averaged mean energies of the three exit particles in the t(t,2n)a reaction are handled differently, because at any given initial particle total energy, the center-of-mass energies of the exit particles are distributed, rather than sharply clustered at a single value. This is because this reaction proceeds partly by instantaneous three-particle breakup, and partly by a sequence of two-body states. In the latter process 5He is formed by the t(t,n)5He reaction, and then breaks up into a neutron and an alpha while in flight.
In the current version of the TDF system, we estimate the mean energies of the exit particles in the center-of-mass frame for the t(t,2n)a reaction by calculating the expectations of their energies over the final state energy distributions that were experimentally measured at LLNL by Wong, Anderson and McClure (1965). They directed a 500 keV beam of tritons on a tritium target and measured the energy spectrum of the neutrons and alphas emitted perpendicular to the beam line. The resulting center-of-mass frame neutron and alpha energy distributions suggested that the t(t,2n)a reaction proceeded 70% by direct three-body breakup, and 30% by sequential two-body final states, first by the t(t,n)5He reaction, then by breakup of 5He in flight into an alpha and a neutron. The 30% sequential breakup distribution was further estimated to subdivide into two competing processes in which 5He was either left in the ground state (20% of the time) or in a broad first excited state at 2 MeV (10% of the time). (This first excited state has subsequently been assigned a level energy of 4 MeV, see Ajzenberg-Selove (1988)). Each one of these three processes (channels) results in different mean energies for the two neutrons and alpha particle. The mean energies of these particles for all reaction processes are therefore their expectation energies, which are the sum of their mean energies in each process weighted by the relative frequency of each process.
If we make the simplifying assumption that these branching ratios hold for the t(t,2n)a reaction in a warm plasma, then the mean energies of the exit particles can be approximately modeled in a relatively straightforward manner. We first consider the reaction kinetics at zero plasma temperature, for then the center-of-mass frame is at rest and the emitted particle energies take on simple and well-defined distributions. In the simultaneous three-body breakup process, the exit particles each have a phase space spectral energy distribution of the form
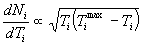
where
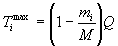 ,
,
M is the sum of the particle masses, and i = 3, 4 and 5. (This corresponds to the two neutrons and one alpha particle of the t(t,2n)a reaction). The average of the particle energies over this symmetric distribution is obviously
In the sequential two-body final state mode, the first final state is the "usual" two-body case, and the energies of the emitted particles are
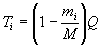
for i = 3 and 4 (corresponding to the neutron and 5He nucleus of the t(t,n)5He reaction). Their energy distributions
are very sharp, so  for i = 3, 4. The second final state
occurs when the heavier particle (say, m4)
breaks up in flight into two particles, say m5 and m6 (corresponding to a neutron and an
alpha particle), and releases breakup energy QB in the process. The exit particles
in this stage have a uniform (boxcar) distribution of energies between two
limits, which are given (for, e.g., particle 5) by the relations
for i = 3, 4. The second final state
occurs when the heavier particle (say, m4)
breaks up in flight into two particles, say m5 and m6 (corresponding to a neutron and an
alpha particle), and releases breakup energy QB in the process. The exit particles
in this stage have a uniform (boxcar) distribution of energies between two
limits, which are given (for, e.g., particle 5) by the relations
The average particle energy over this distribution is evidently
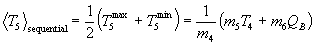 .
.
For the t(t,2n)a reaction, the Q value is 11.33 MeV, and there are two known competing sequential two-body final states corresponding to 5He left in the ground state and in a broad first excited state at 4 ± 1 MeV (Ajzenberg-Selove, 1988). The breakup energy (QB) for 5He in the ground state is .89 MeV, and for the first excited state it is approximately 4.89 MeV. The mean particle energies (i.e. the average over that particle energy distribution) for each channel of this reaction are calculated from the above expressions, and the results are presented in the following Table I.
| channel and fraction (bi) |
|
|
|
Ex(5He) |
| three-body breakup (70%) |
4.718 |
4.718 |
1.906 |
- |
| 1st sequential two-body (20%) |
8.694 |
1.066 |
1.589 |
0 |
| 2nd sequential two-body (10%) |
5.363 |
4.124 |
1.854 |
4 ± 1 |
| weighted mean, 3 channels |
5.577 |
3.928 |
1.838 |
- |
Table I. Mean center-of-mass frame energies (MeV) for
t(t,2n)a exit particle distributions in each channel
The last line in the table gives the weighted mean energies of each particle over all reaction channels. These are calculated from their expectation sum, which is
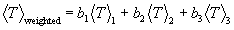 ,
,
where the subscript i is the channel label, 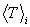 is the particle energy for each channel
averaged over the particle's distribution, and the branching ratio fractions
bi for each channel (also
given in the table) sum to unity: b1 + b2 +
b3 = 1.
is the particle energy for each channel
averaged over the particle's distribution, and the branching ratio fractions
bi for each channel (also
given in the table) sum to unity: b1 + b2 +
b3 = 1.
We estimate the reaction-averaged energies of the three exit
particles as a function of plasma temperature by the following model, which
is used in the TDF system until a more comprehensive and correct treatment
of three-body final state energetics in a warm plasma is developed. The three
weighted mean center-of-mass energies in the table add up to the final state
total kinetic energy, which is the Q value. This corresponds to a plasma
at zero temperature. The partition fraction that each exit particle i has
of this total energy is fi = 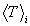 /Q, so for the three particles we
have fn1 = 0.492 ± .007, fn2 = 0.347 ±. 007 and fa = 0.162 ± 001.
The uncertainties are due to the ± 1 MeV uncertainty in the energy level of
the first excited state of 5He. We now assume in our approximation
model that these same fractions fi (of the reaction-averaged final state
total energy) also determine the reaction-averaged energy of the exit particles
for any plasma temperature (White, 1990). That is, for any given q
we calculate
/Q, so for the three particles we
have fn1 = 0.492 ± .007, fn2 = 0.347 ±. 007 and fa = 0.162 ± 001.
The uncertainties are due to the ± 1 MeV uncertainty in the energy level of
the first excited state of 5He. We now assume in our approximation
model that these same fractions fi (of the reaction-averaged final state
total energy) also determine the reaction-averaged energy of the exit particles
for any plasma temperature (White, 1990). That is, for any given q
we calculate 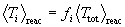 for each exit particle i, where
for each exit particle i, where
and where subscripts 3, 4 and 5 correspond to n1, n2 and a. Then the reaction-averaged mean kinetic energies of each
exit particle are assumed to have the values 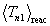 = 0.492
= 0.492 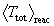 ,
,
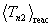 = 0.347
= 0.347 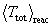 , and
, and
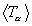 = 0.161
= 0.161 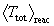 at that plasma temperature.
at that plasma temperature.
The procedure is thus to first calculate 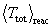 for a given q,
and then use the above partition fractions to estimate the three final state
particle
for a given q,
and then use the above partition fractions to estimate the three final state
particle 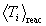 values. These fractions are "hard-wired"
into the TDF system mean energy lookup routine for the t(t,2n)a reaction. It is expected that these averaged
energy estimates — as derived from the partition fractions — will be revised
(perhaps minimally) when a correct three-body final state reaction formalism
is eventually developed for the TDF system.
values. These fractions are "hard-wired"
into the TDF system mean energy lookup routine for the t(t,2n)a reaction. It is expected that these averaged
energy estimates — as derived from the partition fractions — will be revised
(perhaps minimally) when a correct three-body final state reaction formalism
is eventually developed for the TDF system.
The t(t,2n)a reaction partition fractions used in earlier versions of the TDF system differ slightly from the ones given above: they are fn1 = 0.473, fn2 = 0.364,and fa = 0.163. The reason for this is that a final state consisting of three sequential two-body final state channels was used to calculate the partitioning, and the three-body breakup mode was not considered. The 5He nucleus was assumed to have its first and second excited states at 4 and 8 MeV, so that three channels corresponded to the ground, first and second energy levels. These channels were each assumed to occur with an equal probability of 1/3. These older partition fractions appear close enough to the correct ones to have caused little error in their use.
5. Maxwellian-averaged two-body final state reaction particle spectra
In the center of mass system of two reacting nuclei the kinetic energies of each particle are given by T1¢ = m2TR/M and T2¢ = m1TR/M where TR = T1 + T2 - Tcm. If the final state contains two particles, their center-of-mass energies are then, just as simply, T3¢ = m4(TR +Q)/M and T4¢ = m3(TR +Q)/M. In the limit of a very cold plasma (i.e., q @ 0) the kinetic energies of these exit nuclei would be T3¢ = m4Q/M and T4¢ = m3Q/M. Such energies are sharply defined, and diagnostic measurements would show them to have a very narrow energy spread. In progressively warmer plasmas, i.e., as q increases, the energy spread around these values and the centroid of the distribution also increases; each final state particle energy becomes distributed over some energy range, and thus develops into an energy spectrum that is characteristic of the reaction and the plasma.
In this section we outline a practical analytic integral approach to deterministically calculating this energy spectrum for a thermonuclear reaction in a Maxwellian plasma, which is used in the TDF system. This approach was reported by Williams, and much of the development which follows was taken from his paper (Williams 1971). Williams defines a "super-distribution" for two-body final state nuclear reactions in a plasma with a function f(v1,v2,v3,v4), which measures the probability that the reaction has occurred in such a way that the initial two particles have vector velocities v1 and v2, and the final two particles have vector velocities v3 and v4. Then the probability that the reaction does occur at all — for any values of v3 and v4 — is necessarily given by the following integral result:
where s is the total reaction cross-section corresponding to the initial two particles having the velocities v1 and v2 (or relative velocity vR = |v1 -v2|). To ensure conservation of energy and momentum in the reaction process, Williams redefines f(v1,v2,v3,v4) by implicitly defining a new function g(v1,v2), as follows:
This form is substituted in the above integral and the integration carried out, making full use of the d function properties. This results in the following "normalization function":
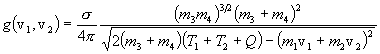 .
.
When the above expressions for s, f and g are combined, we have a redefined
form for s to insert in the
integral which formally defines 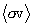 , which is
, which is
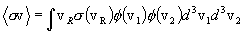 ,
,
or, a little more explicitly,
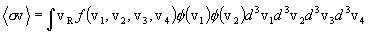 .
.
We now employ a useful short cut developed by Williams: we "unpeel" from this multiple integral the presumed rate of production of final state particle 3, by formally omitting the integration over d3v3 to obtain the distribution
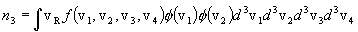 .
.
This is formally equal to the number of particle 3's produced in the reaction
with velocity v3 within cell d3v3in velocity space; the integral of
n3d3v3
recovers the full statistically averaged reaction rate 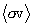 . It is also clear that n3
contains the spectral information associated with the plasma and its distribution
functions f(vi).
We bring this out more explicitly by noting that the directivity in the production
of particle 3 in the plasma is isotropic; the basis for this assumption was
presented in Section 3 and is discussed more fully at the end of this section.
Then the angular part of the integral of can be carried out with the result
that
. It is also clear that n3
contains the spectral information associated with the plasma and its distribution
functions f(vi).
We bring this out more explicitly by noting that the directivity in the production
of particle 3 in the plasma is isotropic; the basis for this assumption was
presented in Section 3 and is discussed more fully at the end of this section.
Then the angular part of the integral of can be carried out with the result
that
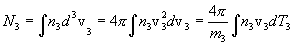 .
.
Because dT3 is the integration element, we can identify the last integrand as the spectral energy density of reaction product particle 3 in the plasma; it is the number of particle 3's produced with energy T3 in the interval dT3 per unit volume per unit time. Thus the particle 3 spectral rate density is
This is the formal expression of the energy spectrum of the emission of particle 3 in the isotropic plasma. The evaluation of the integral for n3 results in the explicit numerically integrable expression for the energy spectrum dN3/dT3 of particle 3 as a function of its energy. The full formal expression of the integral for dN3/dT3 is therefore as follows:
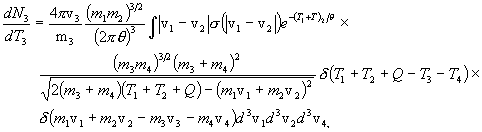
where we have replaced the general plasma particle distribution functions f(vi) by the Maxwellian forms f(mi,vi,q), as given previously in Section 2.
We sketch here only briefly the procedures we used to reduce this formidable integral. We first express all velocities in terms of v3, vcm, and vR, and then carry out the integration over d3v4, utilizing the momentum d function in the process. Two integrals result, with vcm and vR as the variables of integration. which are not totally separated because the energy d function argument contains both variables. However this argument does contain the cosine of the angle between v3 and vcm, so the angular part of the vcm integral is evaluated using v3 as the z-axis, while "using up" this d function. Then the integration is carried out over vcm. The "final result", representing much algebra and evaluation of the energy d function over finite angle limits (see Appendix C), is a single integral over the variable TR, as follows:
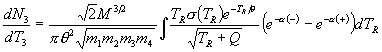
where the exponents are given by
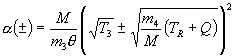 .
.
The functional dependence of dN3/dT3 on T3
is now clearly evident. In fact, if we integrate dN3/dT3 over dT3 we indeed recover 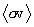 , as we should. (This integral was also
presented by Talley and Hale (1988) but without elaboration.)
, as we should. (This integral was also
presented by Talley and Hale (1988) but without elaboration.)
Because of particle symmetry in the equations, we obtain the spectral energy distribution for particle 4 from the above merely by switching labels 3 and 4 in all of the preceding derivation. dN4/dT4 is obtained, as it were, "by inspection."
Note that the exponents in the above integral can be rewritten as
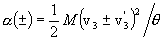 ,
,
and since vcm = v3 - v3¢ we can have, alternatively,
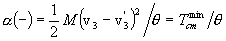
corresponding to the cases where v3
and v3¢ are parallel or antiparallel, respectively.
Also, 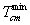 and
and 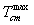 as defined above are the limits for the
integration over dTcm , which in turn come from the angular integration of
the energy d function over
the direction cosine of vcm, or cosqcm.
This angular integration is carried out by the steps shown in Appendix C.
as defined above are the limits for the
integration over dTcm , which in turn come from the angular integration of
the energy d function over
the direction cosine of vcm, or cosqcm.
This angular integration is carried out by the steps shown in Appendix C.
We close this section with the resolution of a subtle and historically persistent issue. Our definition of the f and g functions given above was taken from Williams (1971) and contains the total cross-section s rather than the differential cross-section ds/dW. This implies a priori that the details of the reaction angular distribution do not affect particle spectra. Heinrichs et al (1989) included this angular distribution explicitly in their formulation, and obtained an integral for the particle spectra similar but not identical to Williams'. Their spectrum integral also contains s, and they assert that it depends in no way on the angular variation of ds/dW. Perkins (1990) addressed this angular anisotropy issue by carrying out Monte Carlo calculations of two-body final state energy distributions for reactions having markedly non-isotropic differential cross-sections ds/dW. He found empirically that the angular variation of ds/dWhad no effect on the final state particle spectra.
This anisotropy issue is actually moot. We observe that s rather than ds/dW occurs in all joint distribution functions treated here, because s is the probability for the thermonuclear reaction to occur at all. It therefore selects, as it were, only that subset of the particle population in the plasma that participates in the reaction, and it thereby defines the reaction distributions. This selection is independent of final state properties, that is, it holds for any final state configuration that can occur. At no point does the angular distribution of the final state particles become a factor. Both F in Section 3 and g(v1,v2) in this section have this independence property. The angular properties of the final state in the Maxwellian plasma — which is inherently isotropic to begin with — are determined by the conservation laws, and these are put into effect by the delta functions in the integrand of the spectral distribution functions dNi/dTi. The statistical reaction average of the direction cosines as treated in Section 3 also vanishes for this same reason.
6. Digression on two-body final state spectrum moments
The integral defining the two-body final state spectrum distribution
dN3/dT3 can be used to work out the moments
of this distribution directly without actually evaluating it, because the
exit particle energy T3
appears only in the part of the integrand which is the difference of two exponentials.
The general integral for the nth
moment of the spectral distribution is the spectral expectation average of
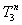 , or
, or
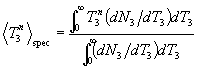 .
.
The actual integral over dT3 that is needed to work out these moments is
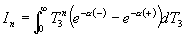
where a(±) is as given in the previous section.
This integral In is used to evaluate both the numerator
and denominator of the expression for 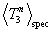 because, evidently,
because, evidently,
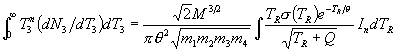 ,
,
and the case n = 0 applies to the denominator. Although the multipliers in front of the integrals can cancel out in the ratio, they are not discarded here.
There exist different algebraic approaches for evaluating these
auxiliary moment integrals In.
The one we use is to first make the substitution 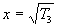 and rewrite the integral in the form
and rewrite the integral in the form
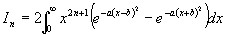
where 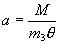 and
and 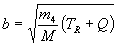 . We reconsider this as the difference of
two separate integrals In = I- -
I+ where the new
ones are
. We reconsider this as the difference of
two separate integrals In = I- -
I+ where the new
ones are
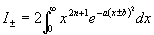 .
.
These integrals are simplified further by making the substitutions u = x + b in I+ and u = x - b in I-. The results are
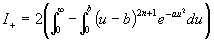
and
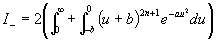 .
.
When these two integrals are subtracted, the finite integrals combine to zero, leaving the result
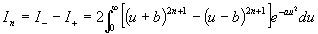 .
.
This reduces (for any given n) to well-known definite integrals when the difference term is expanded and simplified further.
We are interested particularly in In for the cases n = 0 and n = 1, which evaluate to
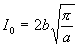 and
and 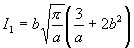 .
.
Higher moment integrals may be evaluated similarly. On replacing a and b with their original meanings, carrying out algebraic reductions, and inserting the results appropriately in the moment integrals, we find – as we asserted earlier – that
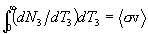
which is the denominator of 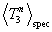 . It is also the numerator for the zeroth
moment
. It is also the numerator for the zeroth
moment 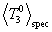 and the area under the spectrum distribution
curve dN3/dT3. Straightforward algebra then produces
the following result for the first moment of the spectrum distribution:
and the area under the spectrum distribution
curve dN3/dT3. Straightforward algebra then produces
the following result for the first moment of the spectrum distribution:
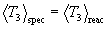
where 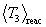 is as given in Section 3. In other words,
the zeroth spectrum moment is obviously unity, and the first spectrum moment
is the reaction statistical average of the final state particle kinetic energy
T3. This is to be expected: the first
moment of a distribution is the mean. Thus we have evaluated the mean exit
particle energy by explicit use of the exit particle spectrum distribution.
These spectrum average results were also derived by Williams (1971).
is as given in Section 3. In other words,
the zeroth spectrum moment is obviously unity, and the first spectrum moment
is the reaction statistical average of the final state particle kinetic energy
T3. This is to be expected: the first
moment of a distribution is the mean. Thus we have evaluated the mean exit
particle energy by explicit use of the exit particle spectrum distribution.
These spectrum average results were also derived by Williams (1971).
7. Data, algorithmic bases and results of 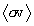 calculations
calculations
The Thermonuclear Data File (TDF) system as currently implemented uses the cross-section data for five exothermic hydrogen and helium nuclear reactions, which are listed with their Q values as follows:
d(d,n)3He Q = 3.26891 MeV
d(d,p)t 4.03271
t(t,2n)a 11.3321
t(d,n)a 17.5894
3He(d,p)a 18.3532
In Figure 3 we show log-log plots of the total reaction cross-section s(TR) for each of these reactions as a function of the relative kinetic energy TR of the two initial particles in their center-of-mass system, from about 100 eV to 15 MeV. This laboratory frame cross-section data was provided by the LLNL Nuclear Data Group (White, 1990). These are the cross-section functions that are used in all integration procedures described in this report.
Because of the smoothness of these data in log-log space, all interpolations and lookups on these cross-sections are carried out by the cubic Lagrange technique, which provides extremely smooth and highly accurate results even though logarithmic and exponential operations are used. The cubic Lagrange interpolation procedure fits a cubic in Lagrange form through four points, and then the interpolation is carried out between the two inner points. The Lagrange interpolating cubic function has the following form:
|
f(x) = |
f1(x - x2)(x - x3)(x - x4)/((x1 - x2)(x1
- x3)(x1 - x4)) + f2(x - x1)(x - x3)(x - x4)/((x2 - x1)(x2 - x3)(x2 - x4)) + f3(x - x1)(x - x2)(x - x4)/((x3 - x1)(x3 - x2)(x3 - x4)) + f4(x - x1)(x - x2)(x - x3)/((x4 - x1)(x4 - x2)(x4 - x3)) |
where f1, f2, f3 and f4 are the values of the interpolant data at the points x1, x2, x3, and x4. In the case of the cross-section data in the TDF system we use ln s(TR) for the fi and ln TR for the xi. The four adjacent ln TR entries in this array used to construct the cubic are chosen so that the interpolating point lies between the middle two. The LLNL cross-section file energies are spaced so that linear interpolation of the cross-section as a function of energy is accurate to within 1 %. Using the cubic Lagrange procedure on this array in log-log space in the manner just described can provide an interpolation accuracy of the order of 10-5, i.e. .001 %.
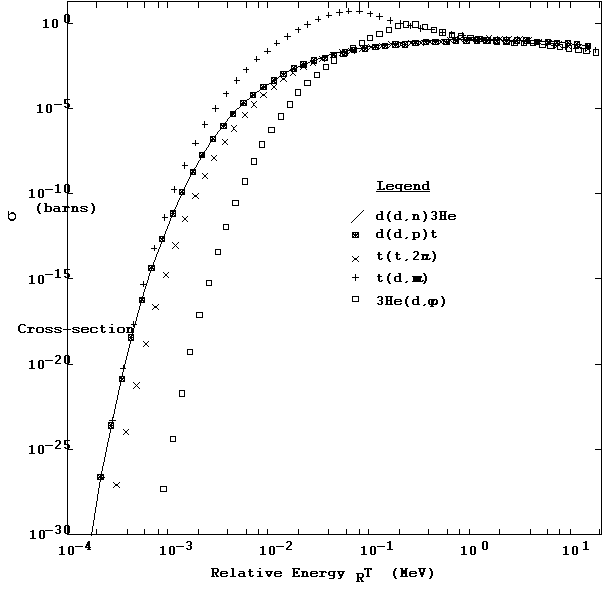
Figure 3. Total cross-section for five TDF reactions
The Gamow function integrands for the Maxwellian-averaged reaction
rates 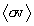 are similarly smooth, and typical cases
are shown in Figure 4 for — by way of example — the t(d,n)a reaction at three different Maxwellian plasma
temperatures. The cross-section function for this reaction — which is part
of the integrands — is also displayed for comparison.
are similarly smooth, and typical cases
are shown in Figure 4 for — by way of example — the t(d,n)a reaction at three different Maxwellian plasma
temperatures. The cross-section function for this reaction — which is part
of the integrands — is also displayed for comparison.
These integrand functions are displayed again in Figure 5 in
a linear-linear plot, but this time renormalized to the same peak value, in
order to show off differences in form and width for different plasma temperatures.
From Figures 4 and 5 it is seen that the maximum contribution to the 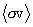 integral comes from progressively larger
values of s and TR
as the plasma temperature qincreases.
integral comes from progressively larger
values of s and TR
as the plasma temperature qincreases.
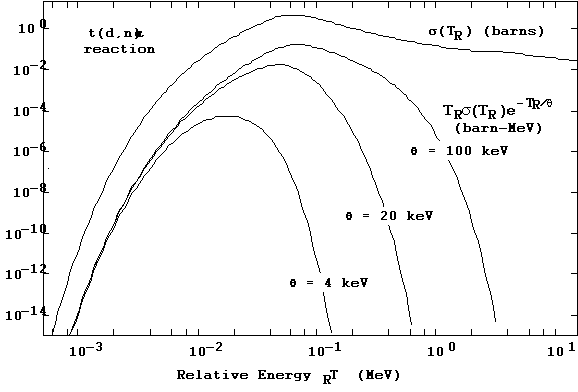
Figure 4. Gamow integrand functions and cross-section data
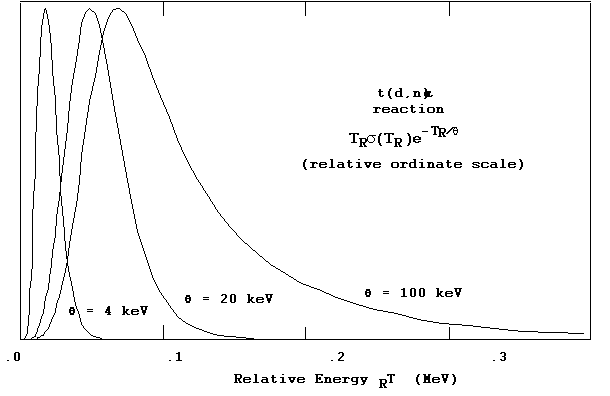
Figure 5. Linear-linear plot of Gamow integrands.
The integration procedure used to calculate 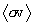 is
illustrated schematically in Figure 6. For a given temperature q, the energy TR and value at which the Gamow integrand
function peaks is determined by table lookup, and the two values of TR at which the function is at 10-4 of this peak are calculated by Newtonian
root iteration. These two values (
is
illustrated schematically in Figure 6. For a given temperature q, the energy TR and value at which the Gamow integrand
function peaks is determined by table lookup, and the two values of TR at which the function is at 10-4 of this peak are calculated by Newtonian
root iteration. These two values (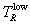 and
and 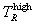 ) determine three integration
intervals. The integration over the middle (main) interval between
) determine three integration
intervals. The integration over the middle (main) interval between 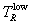 and
and 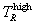 is carried out by one or two 16-point Gauss-Legendre
quadratures, depending on the interval size. The integration from 0 to
is carried out by one or two 16-point Gauss-Legendre
quadratures, depending on the interval size. The integration from 0 to 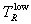 is done by fitting a power law function
of TR to the
integrand over this interval, and integrating that function. The integration
from
is done by fitting a power law function
of TR to the
integrand over this interval, and integrating that function. The integration
from 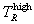 to ∞ is done by fitting an exponential
in TR to the
integrand over that range, and integrating that function. The integral for
to ∞ is done by fitting an exponential
in TR to the
integrand over that range, and integrating that function. The integral for
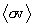 is
then the sum of these three integration results. The accuracy of this approach
has been verified to six places by using it to evaluate integrals of tz-1e-tdt and t-ne-ztdt,
and comparing answers with published values of the Gamma function G(z) and exponential integrals En(z). (The integral of
is
then the sum of these three integration results. The accuracy of this approach
has been verified to six places by using it to evaluate integrals of tz-1e-tdt and t-ne-ztdt,
and comparing answers with published values of the Gamma function G(z) and exponential integrals En(z). (The integral of 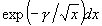 was also accurately evaluated as
a special case of En(x).)
was also accurately evaluated as
a special case of En(x).)
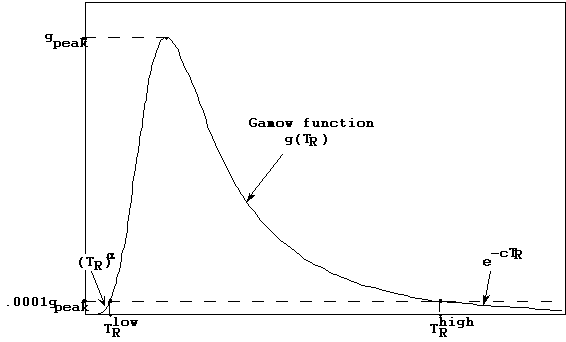
Figure 6. Gamow function integration intervals
There are three other practical reasons for preferring this algorithmic approach to the integration. First, only the relevant range of the integration variable TR is used, as opposed to doing the numerical integration over the entire data range; the integration is thus efficient and also minimizes computational noise. Second, this integration procedure is well-suited to the other Maxwellian-distribution type integrals required for the TDF system, and is also used for them. Third, this integration technique is extremely fast, and permits function lookups and iterative root findings by direct integration, rather than by interpolation over pre-calculated arrays. It thereby facilitates accurate numerical double integration required to generate the output particle energy spectrum quantities.
The results for the reaction rate integration for the five TDF
system nuclear reactions are shown in Figure 7, in which  is plotted as a function of the plasma temperature
from 1 keV to 1 MeV for each reaction. As with the cross-sections, the reaction
rates also range over several orders of magnitude.
is plotted as a function of the plasma temperature
from 1 keV to 1 MeV for each reaction. As with the cross-sections, the reaction
rates also range over several orders of magnitude.
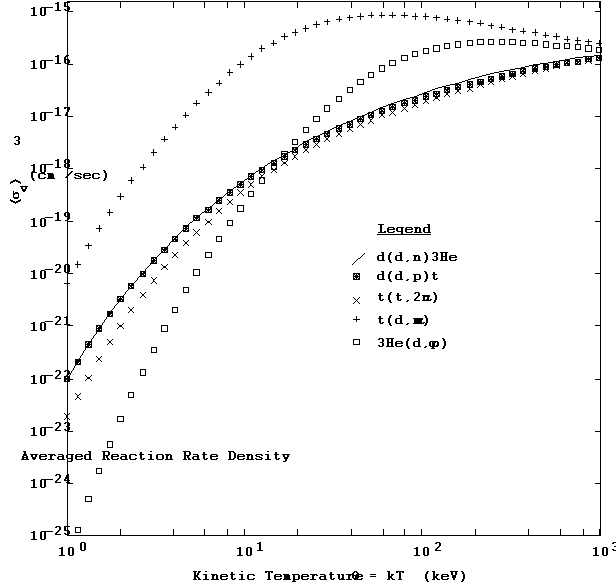
Figure 7. Reaction rate  for five TDF reactions as
for five TDF reactions as
a function of the plasma kinetic temperature.
Previous calculations of  have been carried out by many authors.
The ones done at LLNL prior to the current TDF system have been reported by
Greene (1967) and Howerton (1979). The generation and use of
have been carried out by many authors.
The ones done at LLNL prior to the current TDF system have been reported by
Greene (1967) and Howerton (1979). The generation and use of 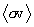 in stellar nucleosynthetic and other astrophysical
contexts is outlined, for example, by Caughlan and Fowler in their 1988 compilation
and earlier papers.
in stellar nucleosynthetic and other astrophysical
contexts is outlined, for example, by Caughlan and Fowler in their 1988 compilation
and earlier papers.
8. Algorithmic bases and results for 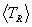 ,
,
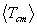 and
and 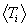
The Maxwell-averaging integrals used to calculate the mean particle
energies and final state spectra are evaluated in the same manner as for the
reaction rates; the integrands are morphologically identical. In Figure
8 we show — using the d(d,n)3He
reaction in a 100 keV plasma as an example — the functional forms of the integrands
for the reaction rate 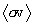 , the mean relative initial state kinetic
energy
, the mean relative initial state kinetic
energy 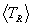 (which is used in obtaining all the
(which is used in obtaining all the 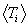 ), and the Maxwellian-broadened energy spectrum
for each final state particle. The integration procedure for the Gamow function
described in Section 7 and illustrated in Figure 6 applies equally well to
these other integrands.
), and the Maxwellian-broadened energy spectrum
for each final state particle. The integration procedure for the Gamow function
described in Section 7 and illustrated in Figure 6 applies equally well to
these other integrands.
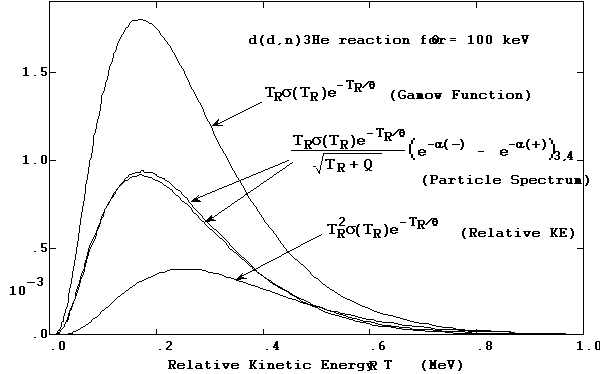
Figure 8. Integrand function forms for the Maxwell-averaging procedures,
using the d(d,n)3He reaction in a 100 keV plasma to create this example.
For the Maxwellian averaged mean particle energies only the averaged
values of TR and Tcm are required since the 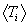 are linear combinations of
are linear combinations of 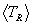 and
and 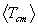 = 3q/2, and
= 3q/2, and 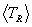 is the only average requiring an integration.
Example results are shown in Figure 9 as plots of
is the only average requiring an integration.
Example results are shown in Figure 9 as plots of 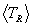 ,
, 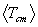 and the
and the 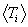 for i = 1, 2, 3, 4 versus plasma temperature
q, for the d(d,p)t reaction, where
q ranges from 0 to 1000 keV.
The indicial correspondence here is that particles 1 and 2 are d's, particle
3 is a p and particle 4 is a t. For the most part these variations are fairly
linear in q (and
for i = 1, 2, 3, 4 versus plasma temperature
q, for the d(d,p)t reaction, where
q ranges from 0 to 1000 keV.
The indicial correspondence here is that particles 1 and 2 are d's, particle
3 is a p and particle 4 is a t. For the most part these variations are fairly
linear in q (and 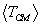 is exactly linear). Indeed, one could approximate
is exactly linear). Indeed, one could approximate
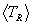 ≈ 2q for this reaction. Note that the values
of
≈ 2q for this reaction. Note that the values
of 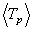 and
and 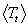 at zero temperature correspond to miQ/(m3 + m4) for i = 4 and 3 (where Q
≈ 4 MeV), as they should.
at zero temperature correspond to miQ/(m3 + m4) for i = 4 and 3 (where Q
≈ 4 MeV), as they should.
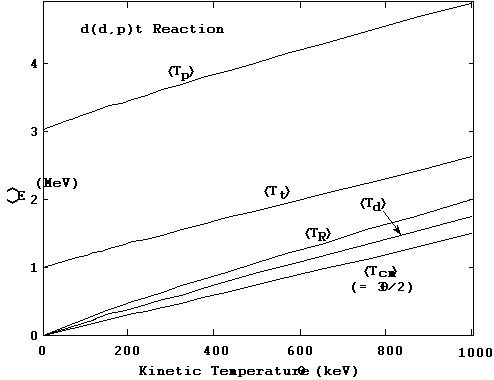
Figure 9. Maxwellian averaged mean particle and system energies
for the d(d,p)t reaction as a function of plasma kinetic temperature.
The integrations for the reaction rate spectral distributions dNi/dTi are likewise straightforward, and handled the same way as the other integrations just described. We show in Figures 10a and 10b the final state energy distributions calculated in the TDF system for the two exit particles in the d(d,p)t reaction. The log-log plots in 10a indicate the stability the TDF integration procedures are capable of, as they show how well the regularity and smoothness of the spectrum functions are maintained over several orders of magnitude.
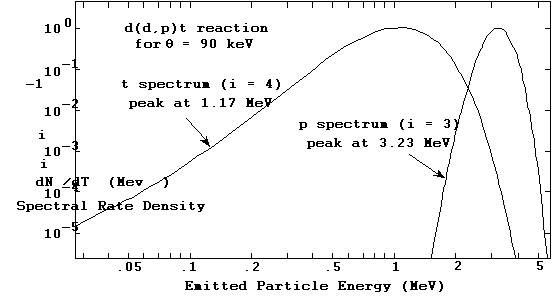
Figure 10a. Final state reaction rate spectral density distribution
for the d(d,p)t reaction at a plasma temperature of 90 keV.
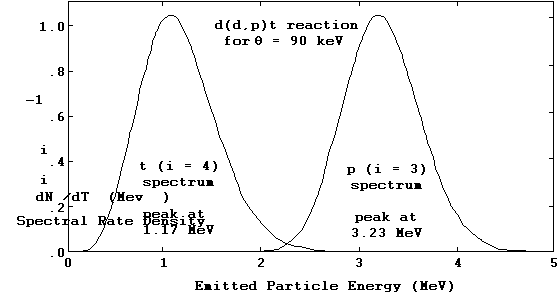
Figure 10b. Final state reaction rate spectral density distribution
for the d(d,p)t reaction at a plasma temperature of 90 keV.
We need to point out that the energy averaging and spectral calculation procedures just described apply only to those TDF system reactions that have two-body final states; the t(t,2n)a reaction, with three particles in the final state, is handled differently. For this reaction no spectral information is provided, as this requires development of three-body final state spectral distributions and their adaptation to thermonuclear plasmas. This will be the subject of a separate and forthcoming report. The reaction-averaged mean energies of the final state particles in the t(t,2n)a reaction, however, are calculated using the approximate multiple channel model developed earlier in Section 4.
9. Algorithmic basis of the final state spectral probability distributions
One of the main uses for final state spectral distribution information is to provide a probabilistic basis for final state configuration sampling in Monte Carlo simulations involving plasma reaction products. The integral over the final state spectral distributions, when treated as a function of the spectral energy, can be used for Monte Carlo sampling. Recall that dNi/dTi is the final state particle spectral distribution function for some particular output particle for a given reaction in a plasma at a given plasma temperature, viz. i = 3 or 4 (or even 5). Let us define a normalized spectral distribution by the function
Then the integral of this normalized distribution as a function of energy is given by
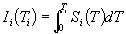 .
.
Because the area under the spectral distribution dNi/dTi is indeed 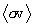 , this monotone integral function is asymptotically
bounded on [0,1], that is, Ii(0)
= 0 and Ii(∞)
= 1. It is therefore suitable for the random statistical sampling over [0,1].
, this monotone integral function is asymptotically
bounded on [0,1], that is, Ii(0)
= 0 and Ii(∞)
= 1. It is therefore suitable for the random statistical sampling over [0,1].
It is very useful to define an auxiliary function ui(Ti) by the relationship
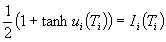 .
.
This is inverted to obtain the following defining functional form for ui:
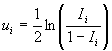 .
.
We also find that an equally convenient relationship defines Si in terms of ui and its first derivative, as follows:
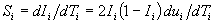 .
.
We show in Figure 11 plots of these three functions for the third particle (the neutron) from the t(d,n)a reaction, at a plasma temperature of 90 keV. The display is in three parts, one for each function, with a common energy abscissa.
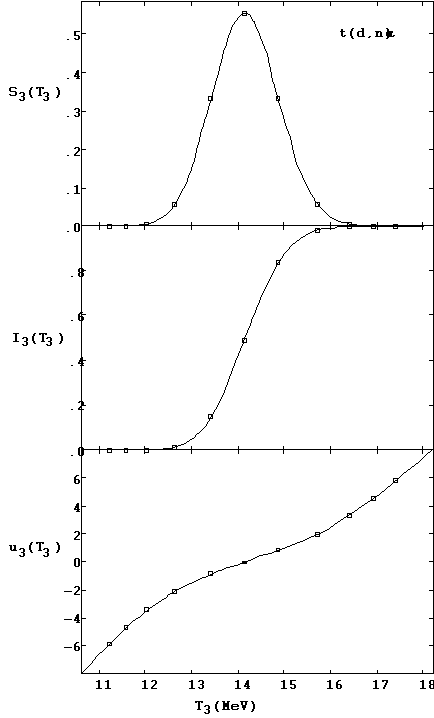
Figure 11. Spectral, probability and auxiliary functions for the
neutron output from the t(d,n)a reaction at 90 keV.
The reasons for using the (1 + tanh) function to reformulate Ii(Ti) are, first, that Ii(Ti) has roughly that form, and, second, the auxiliary variable ui provides a very convenient basis from which to do extremely accurate interpolation over a small collection of points that define the values of Si and Ii as a function of Ti. The way this works in the TDF system is as follows: when an input random number value for Ii is provided, the corresponding ui is determined by calculating ui as a function of Ii. Then we interpolate both dui/dTi and Ti at this ui and obtain Si. The convenience of this arrangement stems from the fact that Ti and ui are very smooth functions of each other over the entire practical energy range, and so the other quantities can be very accurately interpolated — over many orders of magnitude in spectrum amplitude — with very few points. This smoothness appears to be present for all reactions and particle output types in the TDF system. To show the power of this procedure, we used only the 11 points indicated by small squares in each of the first two graphs of Figure 11 to interpolate from, and thus generate all three curves shown.
It is clear that generating the data for the cumulative probability distribution Ii(Ti) requires numerical double integration, and we detail how this is done in the TDF system. For each spectrum at a prearranged given plasma temperature, we chose 11 points on the spectrum curve — at the peak spectrum amplitude and at the spectrum amplitudes at 0.6, .1, .01, .001 and .0001 of the peak value — to be used for the interpolating point set. The particle energies for each of these lower spectrum amplitudes are determined by using Newton's iterative root finding method on each side of the spectrum peak. In using this method every lookup of a spectrum point was done by actually carrying out the integral for the spectrum value at each iteration (rather than by interpolation). We show in Figure 12 these 11 points for the t(d,n)a reaction at a plasma temperature of 90 keV, which are indicated in the figure by the small open squares lying on the spectrum function curve. (The 11 points shown by open squares in each of the three plots in Figure 11 also have the same significance.)
The values of the cumulative probability function Ii(Ti)
at the interpolation energies Ti
are obtained by numerically integrating the function Si(Ti) between each pair of adjacent points,
using Gauss-Legendre quadrature. The Si(Ti) values needed for the quadrature are
obtained by actually doing the integral for the spectrum value dNi/dTi at each quadrature point Ti (as opposed to doing an interpolation)
and normalizing to 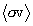 . The double integration is thus in effect
a Gaussian quadrature on the spectrum distribution function with the quadrature
function values determined by Gaussian quadrature on the spectrum integrand.
In this way we obtain the 11 number triplets per spectrum, i.e., S,
T and I, for interpolating the particle energy spectrum S
and particle energy T from the cumulative probability I at a
given plasma temperature. Because of the auxiliary function u, the
results of the spectrum lookups are quite accurate over several orders of
magnitude. This is suggested by the regularity in the semi-log plot of S3(T3) in Figure 12, which follows, over
the range of particle energy and amplitude shown.
. The double integration is thus in effect
a Gaussian quadrature on the spectrum distribution function with the quadrature
function values determined by Gaussian quadrature on the spectrum integrand.
In this way we obtain the 11 number triplets per spectrum, i.e., S,
T and I, for interpolating the particle energy spectrum S
and particle energy T from the cumulative probability I at a
given plasma temperature. Because of the auxiliary function u, the
results of the spectrum lookups are quite accurate over several orders of
magnitude. This is suggested by the regularity in the semi-log plot of S3(T3) in Figure 12, which follows, over
the range of particle energy and amplitude shown.
Figure 12. Calculated spectral distribution function for the
t(d,n)a reaction at a plasma temperature of 90 keV where
the interpolation array points are indicated by open squares.
10. The Thermonuclear Data File (TDF) generator
The Thermonuclear Data File (hereinafter called TDF) is the data base from which thermonuclear reaction rate and output particle spectral information are "looked up" with TDF-based subroutines, which an application code can use to read the file and generate the thermonuclear information it requires. These subroutines reside in an ASCII source code library file called TDFLIB, and are written in Fortran 77. The TDF is created by a Fortran 77 code called TDFMAKER, which carries out the mathematical and integration operations (as described in Sections 2, 3, 4 and 5) to generate data for each reaction and final state particle in the TDF system. This data is placed in the TDF in a particular standard format for lookup operations. In this section we outline briefly what TDFMAKER does, how it is used, and describe some of its key algorithms. The TDF and its lookup routines in TDFLIB will be described in the next two sections.
TDFMAKER requires as input a file identifying the nuclear reactions to be used, and a separate cross-section data file for each nuclear reaction. The content of an example input file is presented in Table II, which shows the identifying textual data for the five thermonuclear reactions d(d,n)3He, d(d,p)t, t(t,2n)a, t(d,n)a and 3He(d,p)a used in the TDF, respectively. Each line corresponds to a reaction. The first item on each line is the designated (unique but arbitrary) reaction identifier index. The second item is the count of the number of final state (exit) particles of the reaction. The next four (or five) items are the alphameric symbols for the incident particle, target particle and exit particles (in order of increasing A). The last item is the name of the file containing the lab bombarding energy and cross-section data for that reaction. TDFMAKER contains accurate nuclear masses of isotopes from A = 1 to A = 20, inclusive, and it can therefore generate the required kinematic data, including the Q-values.
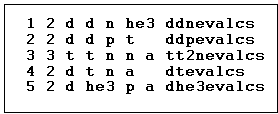
Table II: Example reaction input for the TDFMAKER code.
After reading the input file with the reaction identifiers, TDFMAKER opens each cross-section file and reads in the lab frame beam energy (in Mev) and 4p cross-sections (in barns) for each reaction. The beam energy is converted to center-of-mass energy TR. Both TR and the cross-section s are stored internally as logarithms of their values so as to perform cubic Lagrange interpolation in log-log space. This interpolation technique has proven good to about 5 to 6 significant figures in this application.
TDFMAKER generates the data for the TDF one reaction at a time,
and keeps the generated data for each reaction in separate blocks in the TDF.
After the cross-section data is read in and processed, the value of TR
for the peak of the Gamow function (i.e., the 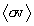 integrand) is calculated as a function of
plasma temperature, since it is used to help determine the three integration
intervals of the numerical integration procedure as depicted in Figure 6.
In what follows we discuss how TDFMAKER is set up to calculate the integrand
peak and the three integration intervals.
integrand) is calculated as a function of
plasma temperature, since it is used to help determine the three integration
intervals of the numerical integration procedure as depicted in Figure 6.
In what follows we discuss how TDFMAKER is set up to calculate the integrand
peak and the three integration intervals.
Gamow's model of Coulomb barrier penetration accounts very well
for the non-resonant variation of thermonuclear reaction cross-sections at
very low energies (Evans, 1955). It is used here to estimate the TR at which the 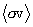 integrand peaks, and to provide an algorithm
for the initial estimate of the numerical integration intervals. A well-known
form of these cross-sections which includes Gamow's model is written as
integrand peaks, and to provide an algorithm
for the initial estimate of the numerical integration intervals. A well-known
form of these cross-sections which includes Gamow's model is written as
where S is a slowly varying function of TR that is very nearly constant at keV energies,
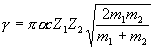
is the Gamow constant, a = 2π e2/hc = 1/137.03604 is the fine structure constant, c is the speed of light, h is Planck's constant, e is the electronic charge, and the Z's and m's are the charge numbers and masses of the reacting isotopes (Evans, 1955). The argument of the exponential is, of course, dimensionless. In the stellar physics field, S(TR) is referred to as the astrophysical S-factor (Chiu 1968, Clayton 1968) and is generally tabulated in cross-section data for stellar nucleosynthesis. Here, for each reaction, we take S to be a constant which normalizes sG(TR) to the reaction s(TR) at low energies. In Figure 13 we plot the cross-sections s(TR) for each reaction, with the corresponding Gamow model cross-section sG(TR) plotted superposed.
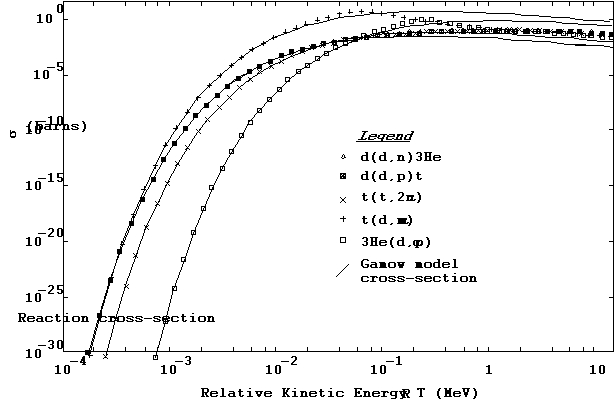
Figure 13. Reaction cross-sections: actual data and
corresponding Gamow analytic model sG for each reaction.
At low energies the fit of sG to the various s's for each reaction is excellent, but deteriorates at the higher energies. To ensure accurate determination of the TR of the peak over all data energies, we use a "variable Gamow constant" scheme in TDFMAKER in which g is calculated at each energy point TR(i) of the cross-section array s(i) so as to make sG fit the data in the neighborhood of that TR. Thus we estimate the "local" value of g at the ith point of the cross-section array as follows:
It is worth mentioning that for all five reactions currently used in the TDF system, g(i) as a function of TR is approximately constant up to about TR = 100 keV, after which it varies significantly with higher values of TR.
When sG
is used in place of s, the
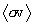 integrand takes the following form:
integrand takes the following form:
 .
.
To find the value of TR at the peak of this function we set ∂G/∂TR = 0 and regard S and g as constants. This results in the following power law relationship between TR of the peak and the kinetic temperatureq:
This recipe (i.e., the power law formula using data-fitted "variable" g) is an excellent peak finder for the Gamow integrand, as shown in Figure 14 for the d(d,p)t reaction and in Figure 15 for the t(d,n)a reaction, where we present a log-log plot of q versus TR at the peak for these reactions in three different ways. The curved line represents the power law with the "variable" recipe for g. The straight line represents the power law with g fixed at Gamow's constant. The symbol ¥ locates the value of TR at which the integrand array calculated for the plasma temperature q actually peaks. The "variable g" recipe appears to provide the best peak predictions, while the "constant g" case does well only at lower values of TR and q.
The data for the d(d,p)t reaction shown in Figure 14 follows the "constant g" power law relationship fairly well over most of its range, but the peak TR values for the t(d,n)a reaction seem to approach an 80 keV asymptote, as shown in Figure 15. (This asymptotic behavior of the peak TR is also evident in Figures 4 and 5.) The reason for this is that the cross-section for the t(d,n)a reaction has a pronounced resonance which carries over into the integrand behavior. Because the TDF system is intended for other reactions which may or may not have resonances, the variable g recipe as given above is included in the TDFMAKER algorithmic lexicon as a permanent feature. This feature and the subsequent integration limit determinations underlie most of the integrations that TDFMAKER carries out, which is the reason why a detailed description of it is included in this report.
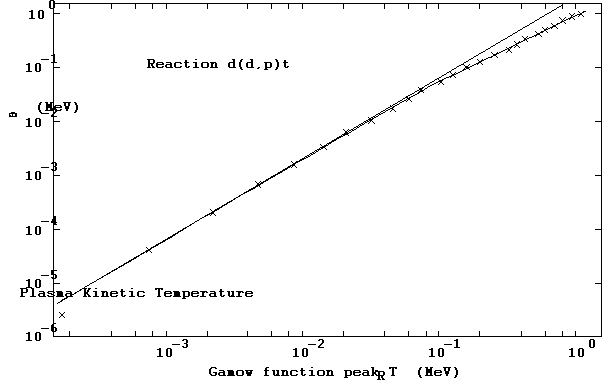
Figure 14. See text for details.
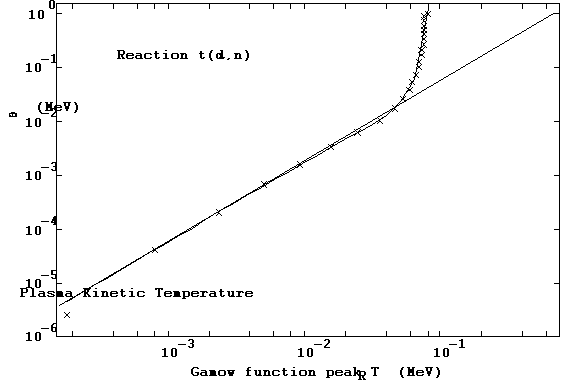
Figure 15. See text for details.
Given, then, that 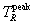 has been determined for a specified q,
we use the Gamow function G(TR,q) of the
has been determined for a specified q,
we use the Gamow function G(TR,q) of the 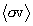 integrand to determine a first estimate
of the two integration interval limits shown in Figure 6. Let e be the fraction of the integrand peak
value at which these limits occur, and denote by TR*
the values of TR
which we estimate by this model to occur at these limits. These are computed
by determining the values of TR* for which the equality
integrand to determine a first estimate
of the two integration interval limits shown in Figure 6. Let e be the fraction of the integrand peak
value at which these limits occur, and denote by TR*
the values of TR
which we estimate by this model to occur at these limits. These are computed
by determining the values of TR* for which the equality
holds. Taking logarithms of both sides gives the algebraic equation
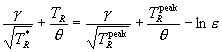 .
.
This is a cubic in the variable 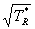 . Rather than solve a cubic, we approximate
the two solutions we need, because at low TR*
the quantity g/
. Rather than solve a cubic, we approximate
the two solutions we need, because at low TR*
the quantity g/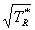 is dominant, while at high TR*
the quantity TR*/q
dominates. Let the right-hand side of this equation be symbolized by q.
Then g/
is dominant, while at high TR*
the quantity TR*/q
dominates. Let the right-hand side of this equation be symbolized by q.
Then g/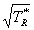 = q defines
= q defines 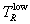 and TR*/q = q defines
and TR*/q = q defines 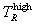 , and we therefore have
, and we therefore have
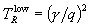
and
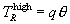 .
.
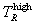 and
and 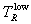 are as depicted in Figure 6, where we recall
that the three integration intervals are 0 to
are as depicted in Figure 6, where we recall
that the three integration intervals are 0 to 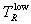 ,
, 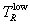 to
to 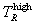 , and
, and 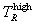 to ∞. In TDFMAKER, e has the value 10-4, and the coding has checks to make sure that
to ∞. In TDFMAKER, e has the value 10-4, and the coding has checks to make sure that 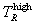 and
and 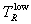 indeed bracket
indeed bracket 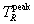 . These interval estimate algorithms are
applied to all the Maxwell-averaging integrals. When this is done, the inner
interval limits are further refined by iterative root finding to be at 10-4 of the peak of the integrand.
. These interval estimate algorithms are
applied to all the Maxwell-averaging integrals. When this is done, the inner
interval limits are further refined by iterative root finding to be at 10-4 of the peak of the integrand.
Recall next that the integrals of the spectrum function dNi/dTi leading to the cumulative probability functions Ii(Ti) are carried out over adjacent particle energy intervals, as outlined in Section 9. Accurate first estimates of the energy at which the spectrum function peaks and the energies bounding each integration interval can be obtained by use of the exponential difference term in the dNi/dTi integrand, which is given by
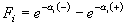 ,
,
where i is the index label (3 or 4) for the particle of interest, the exponents are
and j is the index label (4 or 3) for the other particle. At a given fixed plasma temperature the dependence of Fi on Ti is where the variation of the final state spectrum dNi/dTi with particle energy Ti originates, so Fi determines the shape of dNi/dTi. We also note that Fi is also the integrand for the auxiliary integral In discussed in Section 6 on spectrum moments.
One of the more remarkable insights that emerged during the writing
of this report is the realization that Fi
is a very close approximation to the shape of the spectrum, dNi/dTi, apart from normalization. This is
because the variation of Fi with TR is quite slow, and to a very good approximation
Fi can be taken
outside the integral for dNi/dTi.
In Figures 16a and 16b (as in Figures 10a and 10b) we compare log-log and
linear-linear plots of dNi/dTi and Fi as functions of Ti for the d(d,p)t reaction at q = 90 keV, for both exit particle types. For
these Fi plots TR is set equal to its mean value 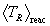 at that temperature. The closeness of the
shapes of dNi/dTi and Fi to each other, for each particle i,
is excellent. We thus obtain very accurate first estimates of the integration
intervals by determining those pairs of energies Ti
that make Fi
equal to the fractions .6, .1, .01, .001, 10-4 and 10-5, since the peak of Fi is very nearly 1. However, because
this approach postdates the TDF system, its implementation is planned for
a future version of TDFMAKER.
at that temperature. The closeness of the
shapes of dNi/dTi and Fi to each other, for each particle i,
is excellent. We thus obtain very accurate first estimates of the integration
intervals by determining those pairs of energies Ti
that make Fi
equal to the fractions .6, .1, .01, .001, 10-4 and 10-5, since the peak of Fi is very nearly 1. However, because
this approach postdates the TDF system, its implementation is planned for
a future version of TDFMAKER.
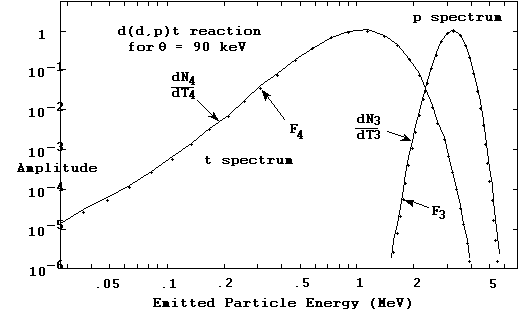
Figure 16a. Spectral distribution dNi/dTi (curved lines) and function
Fi (dots) for the d(d,p)t reaction at a plasma temperature of 90 keV.
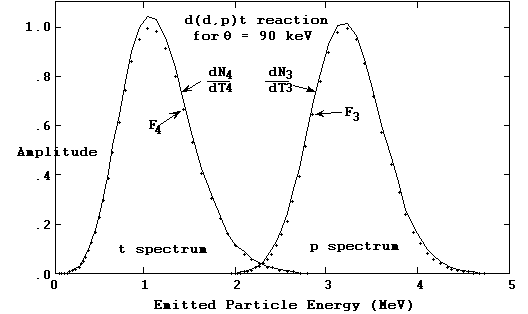
Figure 16b. Spectral distribution dNi/dTi (curved lines) and function
Fi (dots) for the d(d,p)t reaction at a plasma temperature of 90 keV.
The approach originally developed and currently used in TDFMAKER to determine the spectrum integration intervals is based on first inverting the preceding equation for the exponents a to obtain (for, say, i = 3)
TR is set equal
to its value TRpeak at the peak of the integrand, because
this is where the dNi/dTi integrand makes its maximal contribution
to the integral. When a(-)
is zero, a(+) is large, and F3 is almost 1. The resulting value of
T3 estimates the energy of the spectrum
peak, which we denote by 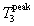 . Next, when a is a large positive number, F3 will be much less than 1, and two values
of T3 (one on
either side of the spectrum peak) result, corresponding to the plus/minus
signs in the parentheses. We estimate the useful energy limits of dN3/dT3 by setting a = ln
104, so that F3
= e-a = 10-4, and we denote the resulting two values
of T3 by
. Next, when a is a large positive number, F3 will be much less than 1, and two values
of T3 (one on
either side of the spectrum peak) result, corresponding to the plus/minus
signs in the parentheses. We estimate the useful energy limits of dN3/dT3 by setting a = ln
104, so that F3
= e-a = 10-4, and we denote the resulting two values
of T3 by 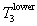 and
and 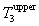 .
.
In the current version of TDFMAKER, these three numbers — 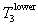 ,
, 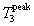 , and
, and 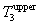 r
— initiate the Newtonian root-finding and peak finder procedures that determine
the value of T3
at which the spectrum peaks, and the T3
pairs (one on each side of the peak) at which the spectrum is at .6, .1, 10-2, 10-3, 10-4 and 10-5 of the peak. These procedures yield the
11 point triples (S, T and I) in the spectrum data arrays for each exit particle
and each plasma temperature that are used to carry out the interpolations
done in connection with Figures 11 and 12 of Section 9. It is between these
values of T3
that the spectrum functions Si(Ti) are integrated to obtain the cumulative
distribution function point values Ii(Ti).
r
— initiate the Newtonian root-finding and peak finder procedures that determine
the value of T3
at which the spectrum peaks, and the T3
pairs (one on each side of the peak) at which the spectrum is at .6, .1, 10-2, 10-3, 10-4 and 10-5 of the peak. These procedures yield the
11 point triples (S, T and I) in the spectrum data arrays for each exit particle
and each plasma temperature that are used to carry out the interpolations
done in connection with Figures 11 and 12 of Section 9. It is between these
values of T3
that the spectrum functions Si(Ti) are integrated to obtain the cumulative
distribution function point values Ii(Ti).
The remainder of TDFMAKER consists of coding and algorithms to
carry out the integrations, inverse lookups (root findings) and maximum findings
described above and referred to in Sections 2 through 9. Two similar Fortran
77 routines in TDFMAKER were written to handle these integrations, one for
the "Gamow peak integrand types" used to calculate 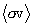 ,
, 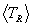 and the spectrum distribution dNi/dTi, and the other to help calculate the
integrals of the dNi/dTi functions used for the spectrum probability
distributions Ii(Ti). The first subroutine (intgrt) is a straight-forward coding of
the integration scheme and limit determinations as described in the previous
paragraphs. The second routine (sp3fn)
is this subroutine intgrt recoded to be a function call and
to carry out only the integration of the spectrum distribution dNi/dTi. This is so that dNi/dTi (in the guise of sp3fn)
is used as a "callable" function within TDFMAKER, as needed. This
"functionality" is what facilitates the high efficiency in carrying
out the integrations over the spectrum distributions, as well as determining
where the maximum of these distributions occur. Subroutine mxfnd
locates the maximum of non-analytic functions by recursively fitting parabolas
to point triplets and calculating the maximum of the parabola. This subroutine
is used to more precisely locate the maximum of the Gamow-type integrands
as well as that of the spectrum distributions.
and the spectrum distribution dNi/dTi, and the other to help calculate the
integrals of the dNi/dTi functions used for the spectrum probability
distributions Ii(Ti). The first subroutine (intgrt) is a straight-forward coding of
the integration scheme and limit determinations as described in the previous
paragraphs. The second routine (sp3fn)
is this subroutine intgrt recoded to be a function call and
to carry out only the integration of the spectrum distribution dNi/dTi. This is so that dNi/dTi (in the guise of sp3fn)
is used as a "callable" function within TDFMAKER, as needed. This
"functionality" is what facilitates the high efficiency in carrying
out the integrations over the spectrum distributions, as well as determining
where the maximum of these distributions occur. Subroutine mxfnd
locates the maximum of non-analytic functions by recursively fitting parabolas
to point triplets and calculating the maximum of the parabola. This subroutine
is used to more precisely locate the maximum of the Gamow-type integrands
as well as that of the spectrum distributions.
Other Fortran 77 subroutines were developed to perform inverse lookup tasks, that is, input the value of a function and output the corresponding argument value by Newtonian root-finding techniques. In TDFMAKER the inverse lookup subroutines all have names beginning with inv. It is within these inverse routines that sp3fn is heavily used as the function value generator in determining energy arguments corresponding to final state particle spectrum distribution values.
11. Structure and content of the TDF
The information in the TDF is in alphameric format so that the TDF can be read as a plain text file. It is therefore platform-independent. The information for each reaction is arranged in separate reaction data blocks within the file, and each block has the same format, which is illustrated by the example of blocks of data from a working TDF that is shown in Appendix A. Every TDF (as of this writing) starts with a header block which is a copy of the input data for TDFMAKER (cf. Table II) that identifies the reactions and the text files containing the reaction cross-section data. Each subsequent reaction data block starts with a line labeling the version of TDFMAKER that was used to generate the block. Within each such block this line is followed by eight different types of sub-blocks of data, each starting with a header line having a unique numeric label in parentheses. The headings for each of these sub-blocks are listed in Table III.

Table III. Data block header lines in the TDF.
Heading line (1) lists the names of the files used by TDFMAKER;
the last one is the name of the TDF itself. This line is followed by an alphameric
identifier code which the TDFLIB subroutines check to insure that they are
reading a compatible version of the TDF. Heading line (2) identifies the
constants on the line which follow it, which are, respectively, the MeV energy
equivalent of the atomic mass unit, the inverse of the fine structure constant,
the speed of light, the Q of the reaction, and the total energies of the final
state particles if those were left in excited states by the reaction. Heading
line (3) identifies the nuclear masses for each particle in the reaction,
in atomic mass units. Heading line (4) identifies two groups of integer data
which follow it. The first five numbers are the isotope identifiers for each
particle in the reaction; these identifiers have the integer value 1000Z
+ A where Z is the nuclear charge (number of protons) and A is the atomic
number (total number of protons and neutrons). The last four numbers are
respectively the number of temperature blocks for each final state particle
spectrum (heading (8)), the number of lines of data in each 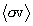 block (heading (5)), the number of final
state particles (a 2 or a 3), and the numerical index/identifier used within
the TDF for that reaction. Heading line (5) identifies the data block containing
the values of q,
block (heading (5)), the number of final
state particles (a 2 or a 3), and the numerical index/identifier used within
the TDF for that reaction. Heading line (5) identifies the data block containing
the values of q, 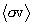 and
and 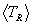 for this reaction. Currently (as shown
in Appendix A) there are 29 lines of these data triplets, each for a different
plasma temperature. Also, there are 13 temperature blocks for each final
state particle spectrum, where each of the 13 blocks corresponds to a different
plasma temperature. Thus if there are two particles in the final state for
a reaction there will be 26 spectrum blocks in that reaction section of the
TDF. The 13 plasma temperatures qi
are the same for all spectrum blocks, and are equal to .0001, .001, .01,
.04, .09, .16, .25, .36, .49, .64, .81, 1.00, and 1.05 MeV. The first and
last temperature entries are included to preserve accuracy of the cubic Lagrange
interpolation within the temperature intervals .001 to .01 and .81 to 1.00.
for this reaction. Currently (as shown
in Appendix A) there are 29 lines of these data triplets, each for a different
plasma temperature. Also, there are 13 temperature blocks for each final
state particle spectrum, where each of the 13 blocks corresponds to a different
plasma temperature. Thus if there are two particles in the final state for
a reaction there will be 26 spectrum blocks in that reaction section of the
TDF. The 13 plasma temperatures qi
are the same for all spectrum blocks, and are equal to .0001, .001, .01,
.04, .09, .16, .25, .36, .49, .64, .81, 1.00, and 1.05 MeV. The first and
last temperature entries are included to preserve accuracy of the cubic Lagrange
interpolation within the temperature intervals .001 to .01 and .81 to 1.00.
The remaining data blocks after line (5) refer to the output
particle spectra. Heading line (6) contains the number of fractions of the
spectrum peak used to define the spectrum interpolation points, and these
fractions are listed in the next line. Heading line (7) identifies (for the
spectrum block which follows) the plasma temperature and the final state particle
index to which the block applies (a 3 or a 4 or (later) a 5), the number of
lines of spectrum data, the integrated area under the spectrum curve, and
the corresponding value of 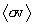 . (A comparison of these last two numbers
gives computational diagnostic information.) Heading line (8) identifies
the spectrum data block and lists, respectively, the line index j and
the values of Tj, Sj and Ij for the given output particle at the
temperature qi specified. These are the actual interpolation
data points used for the spectral information lookups. Currently there are
11 lines of these data quartets per block, corresponding to the peak value
of the spectrum distribution and five pairs of fractional values (currently
0.6, 0.1, 10-2,
10-3, and 10-4) of this spectrum peak value. That is,
S1 = S11 = 10-4 S6, S2
= S10 = 10-3 S6, S3
= S9 = 10-2 S6, S4
= S8 = 0.1 S6, and S5 = S7 = 0.6 S6, where S6 is the peak value.
. (A comparison of these last two numbers
gives computational diagnostic information.) Heading line (8) identifies
the spectrum data block and lists, respectively, the line index j and
the values of Tj, Sj and Ij for the given output particle at the
temperature qi specified. These are the actual interpolation
data points used for the spectral information lookups. Currently there are
11 lines of these data quartets per block, corresponding to the peak value
of the spectrum distribution and five pairs of fractional values (currently
0.6, 0.1, 10-2,
10-3, and 10-4) of this spectrum peak value. That is,
S1 = S11 = 10-4 S6, S2
= S10 = 10-3 S6, S3
= S9 = 10-2 S6, S4
= S8 = 0.1 S6, and S5 = S7 = 0.6 S6, where S6 is the peak value.
As shown in Appendix A, the last five entries of Ij (i.e. index 7 through 11) in each spectrum data block are negative. This is because the numerical value of 1. was subtracted from those Ij in TDFMAKER before putting it out in the TDF, in order to retain the double precision numerical accuracy in the TDF. When these negative numbers are read in by the TDFLIB routines, the value of 1. is added to them to restore them to their original (and positive) double precision value. (TDFMAKER and TDFLIB currently declare double precision for use with 32-bit processors.)
12. The TDFLIB subroutine library
TDFLIB is the name of an ASCII Fortran 77 source program library file that contains 8 subroutines, one function subroutine, and specifications for 3 labeled common blocks. Four subroutines — tdfrdr, mxavlu, speclu, tdmass — and one function subroutine — svblu — are directly used by the applications code that needs the thermonuclear information. Subroutines tdclag, tdchlu, tdmchl and tdselu are specialized interpolation subroutines based on cubic Lagrange and Hermite methods that are intended to be used only by the other subroutines. The three labeled common blocks are tdfcon, tdfsvb and tdfspe; their memory allocation details are spelled out in comments in subroutine tdfrdr.
The main function of the TDFLIB subroutines is to perform monovariate and bivariate interpolations on the condensed data in the TDF, so as to retrieve Maxwellian-averaged and reaction-averaged thermonuclear energy and spectral information, as desired. In what follows, we present a brief description of these subroutines, their argument lists and their purpose, and then follow this by some spectrum data interpolation examples that demonstrate the calculationally robust nature of the TDF system over several orders of magnitude in the variables. Some of these routines were used to generate the plotted data shown in previous sections.
subroutine tdfrdr(iunit,ntr,ierr)
Reads data from the TDF into the three labeled common blocks in memory. It must be called no more than once by the application code before any other routine can be used. iunit is the logical unit number assigned to the TDF by the application code. ntr is the number of thermonuclear reactions read in. ierr is an error flag: zero means that the TDF was read and the memory allocated correctly. A non-zero return means the TDF was not read properly and cannot be used; this is a fatal error indicating that either the TDF was corrupted, or the version of TDFMAKER used to create the TDF, and the current TDFLIB, do not match.
In all the other subroutines, the quantity ierr is a returned error flag, in which zero means that the subroutine call was completed correctly. A non-zero error flag occurring for the main four subroutines and one function usually means that the input reaction or particle index, or one or more input numerical values, was improperly specified. In some cases, however, a more serious error could be indicated. The error flags are explained in the documentation for TDFLIB (White, Warshaw and Resler, 1990).
subroutine tdmass(ireac,bm1,bm2,bm3,bm4,bm5,q,ierr)
Returns purely nuclear masses (i.e. atomic mass minus electron masses and electron binding energies) and the Q-value q (in MeV) for a specified reaction ireac. The mass units are in amu where 12C = 12 amu.
bm1 = mass of lighter reacting particle
bm2 = mass of heavier reacting particle
bm3 = mass of lightest product particle
bm4 = mass of next lightest product particle
bm5 = zero for two-body final state reactions, else is the mass of the remaining product particle in three-body final state reactions
subroutine mxavlu(ireac,tp,sv,e1,e2,e3,e4,e5,ierr)
Returns the Maxwellian-averaged reaction rate sv (cm3/sec) and reaction-averaged kinetic energy (MeV) of the reacting and final particles for the specified reaction ireac and plasma temperature tp (keV).
e1 = kinetic energy of the first reacting particle
e2 = kinetic energy of the second reacting particle
e3 = kinetic energy of the first final particle
e4 = kinetic energy of the second final particle
e5 = zero for 2-body final state reaction or kinetic energy of third final particle
mxavlu identifies the data array index
for the specified reaction, and determines the four sequential data temperatures
which bracket the input plasma temperature tp.
It calls tdclag to interpolate
the reaction rate sv at this input temperature, and tdchlu
to interpolate the mean relative kinetic energy er of the two reacting particles. From
this and the plasma temperature it computes the reaction-averaged kinetic
energies of all particles of the reaction, e1
through e5. mxavlu was used to generate the averaged
kinetic energy data plotted in Figure 9, and was modified specifically to
also output the average of TR
for the plot. (Note that er is the 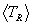 of this report, and the ei
arguments are
of this report, and the ei
arguments are 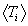 ,
correspondingly.)
,
correspondingly.)
function svblu(ireac,tp,ierr)
Returns the Maxwell-averaged reaction rate svblu (cm3/sec) for the specified reaction ireac and plasma temperature tp (keV). svblu identifies the data array index for the reaction, and determines the four sequential data temperatures which bracket the input temperature tp. It calls tdclag to interpolate the reaction rate over this temperature set. svblu was used to generate the reaction rate plots in Figure 7.
subroutine speclu(ireac,tp,ipart,pin,eout,sout,ierr)
speclu is an inverse particle spectrum lookup routine. Given the input plasma temperature tp (keV) and cumulative probability of emission pin (a real number between 0. and 1.) of exit particle ipart (3 or 4), it returns that particle's energy eout (MeV) and normalized spectral amplitude (i.e., relative probability) sout (MeV-1). The actual spectral amplitude is obtained by multiplying sout by the reaction rate. It is currently implemented for two-body final state reactions only. It returns a non-zero error flag and zero arguments if a reaction with three or more final state particles is selected.
ipart = 3 for the first product particle
ipart = 4 for the second (heavier) product particle
ipart = 5 is intended for a third product particle (not currently implemented)
speclu first checks the range of the input value of pin and returns special values of eout and sout if pin is exactly 0 or 1. For input values of pin between 0 and 1, speclu determines the four sequential data temperatures (and corresponding spectral data blocks in memory) which bracket the user's requested temperature tp. At each of these four temperatures it calls tdselu to interpolate the energy (e) and spectrum amplitude (s) at the user's specified cumulative probability input (pin). The resulting four values each of e and s are then interpolated at the user's specified temperature tp, by calls to tdchlu or tdmchl, as appropriate, and output as eout and sout, respectively. speclu was used to generate the data plotted in figures 10a, 10b, 11, 12, 16a and 16b.
subroutine tdclag(x1,x2,x3,x4,f1,f2,f3,f4,x,fval,ierr)
Cubic Lagrange interpolation routine for mxavlu and svblu. Interpolant x lies between x2 and x3.
subroutine tdselu(nnode,pfnode,ennode,spnode,p,e,s)
Spectrum-energy lookup routine for use by speclu. Input is p, returns are e and s, assuming 0 < p < 1. The formulas developed in Section 9 are used to interpolate e and s over the 11-point data set. Fitted power law and exponential functions are used to extrapolate e and s below and above this data set, respectively.
subroutine tdchlu(x1,x2,x3,x4,f1,f2,f3,f4,x,fval,ierr)
4-point cubic Hermite-Lagrange slope-value interpolation routine for mxavlu and speclu. Interpolant x lies between x2 and x3.
subroutine tdmchl(x1,x2,x3,x4,f1,f2,f3,f4,x,fval,ierr)
Mixed 4-point cubic Hermite-Lagrange slope-value interpolation routine for speclu. Interpolation is in linear space on nodes 1, 2 and 3 and in logarithmic space on nodes 2, 3 and 4. Interpolant x lies between x2 and x3.
The interpolation subroutines in TDFLIB were carefully checked for consistency and robustness before release. One such test was to generate contour plots of the bivariate functions Ii(Si,q) and Ii(Ti,q) for the two output particle spectra (corresponding to i = 3 and i = 4) of each two-body final state reaction, and inspect them for smoothness over the entire variable range in the TDF. The spectrum data (Ti or Si as appropriate) were interpolated from the TDF for 15 probability values Ii and 50 logarithmically spaced values of the plasma temperature q between 1 keV and 1 MeV, thus generating 750 data quartets (q, T, S, I) for each reaction and each output particle. From these quartets for each reaction we chose to generate two types of plots consisting of 15 separate curves, one for each value of I, for each of the two output particles. They are T3 versus q1/2 and T4 versus q1/2 on semi-log scales, and S3 versus qand S4 versus qon log-log scales. These curves are interpreted as contour plots of I.
Four such plots are shown in Figures 17 through 20 for the d(d,p)t reaction, in each of which the 15 contour levels of the cumulative probability function Ii are shown for the two functions, for each output particle. Figures 17 and 18 indicate approximately how the spectrum peak width increases with plasma temperature, where the various curves of Ii define the points on each side of the curve of the peak that are being followed. Figures 19 and 20 are double-sheeted in Ii since at each q there are two values of Ii for every Si.
The essential point of these plots is that none of the 750 interpolated quartets coincide with any of the 143 spectrum data quartets for each reaction output particle in the TDF. Therefore, all calculations of the Ii(Si,q) and Ii(Ti,q) functions for the two output particle spectra are done by bivariate Lagrange and Hermite cubic interpolation over the more limited plasma temperature and spectrum level data points in the TDF. The results are visually excellent over many orders of magnitude. These types of plots were used to choose and "shake down" various bivariate interpolation schemes during the code development phase. The ragged and "noisy" contours that were produced in the early coding stages were the best diagnostic that the interpolation procedures were not performing properly.
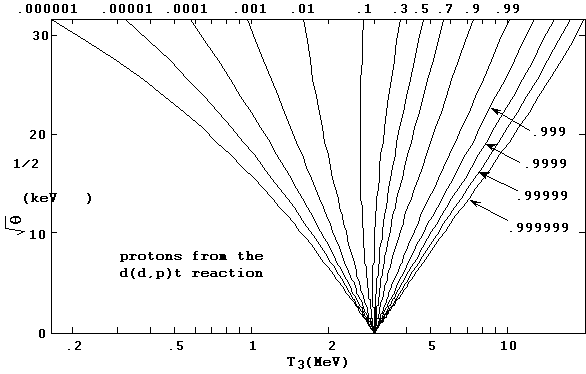
Figure 17. Contours of I3as a function of T3 and q for the d(d,p)t reaction.
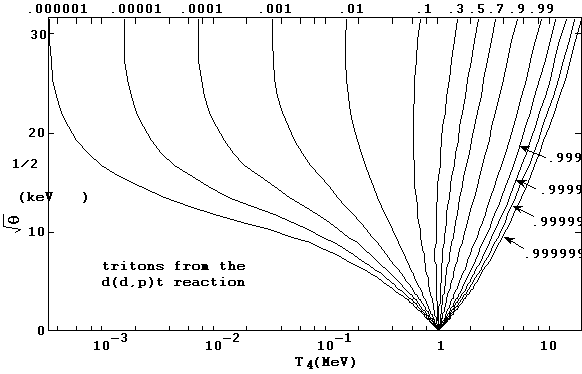
Figure 18. Contours of I4as a function of T4and q for the d(d,p)t reaction.
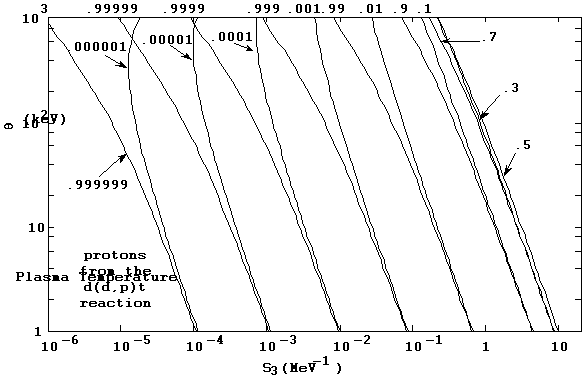
Figure 19. Contours of I3as a function of S3and q for the d(d,p)t reaction.
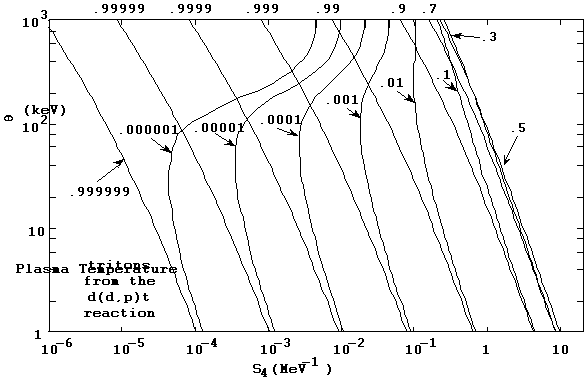
Figure 20. Contours of I4as a function of S4and q for the d(d,p)t reaction.
A word on the nature of the bivariate interpolation used in subroutine speclu is necessary, because it is rather specialized. Given that a plasma temperature q and a cumulative probability value I is input to a spectrum data calculation for a given reaction and a given output particle, the two spectrum data blocks at the two plasma temperatures immediately above and immediately below the input value q is are used to generate, for that input I and those four plasma temperatures qj, four values of the spectrum amplitude Sj and particle kinetic energy Tj. These values of S and T are obtained by cubic Lagrange interpolation over the auxiliary function u that was described earlier in Section 9. For definiteness, we denote these four plasma temperatures by q1, q2, q3, and q4, in monotone increasing value, such that the input value q lies between q2, and q3, and we index the corresponding values of S and T similarly. The required temperature-interpolated values of S and T are obtained by modified cubic Hermite interpolation over the indexed Sand T. The way this is done is to convert the four plasma temperatures to their square root value, qj1/2 and then regard Sj and Tj as functions of qj1/2, where j = 1, 2, 3 and 4. Then the slopes of these functions are modeled at the two inner abscissae — q21/2 and q31/2 — by fitting parabolas to the three points at the abscissa triplets (q11/2, q21/2, q31/2) and (q21/2, q31/2, q41/2). This gives slopes and values for the functions S and T at the inner abscissa pairs q21/2 and q31/2. The cubic Hermite interpolation procedure is then carried out over these slope-value pairs to obtain the values of S and T at the square root of the input q.
The author would like to thank certain people for their assistance and contributions to the development and implementation of the LLNL TDF system described in this report. First, the late Ted Perkins, for bringing the key paper written by Williams (1971) to the author's attention, and for providing his own annotated copy of that paper to the author, with much useful commentary scribbled in the margins. Roger White and David Resler of the Physics Department's former Nuclear Data Group, for providing evaluated nuclear cross-section files and nuclear data subroutines used by the TDFMAKER code to retrieve nuclear masses and reaction cross-sections. Roger White, who, as Nuclear Data Group leader, provided a hospitable environment for development of the TDF system, and Eugene Brooks, who, as the succeeding group leader for Nuclear Data and Codes, provided support for the writing of this report now ten years later. Eugene Canfield, for indicating that the idea of conjoining the nuclear cross-section with the Maxwellian plasma distribution as the required joint distribution for the energy and spectrum averaging may have originated with John von Neumann. And, finally, it is a pleasure to acknowledge the many helpful discussions with and comments made by George Zimmerman, who took a keen interest in the development of the TDF system and its exploratory extensions to include spectra for three-body final state reactions. This report is dedicated to the memory of Sterrett "Ted" Perkins.
References to thermonuclear reaction data and modeling listed here represent neither an extensive nor an exhaustive survey of the field. Rather, they are citations of external and internal reports that the author has found helpful and suggestive in the course of developing the modeling and calculational approaches described in this report. Not all references listed were specifically cited.
F. Ajzenberg-Selove, "Energy levels of light nuclei A = 5 - 10", Nuclear Physics A490, 1 - 225 (1988)
R. E. Brown and N. Jarmie, "Differential Cross-sections at Low Energies for 2H(d,p)3H and 2H(d,n)3He", Physical Review C41, 1391 - 1400 (1990)
R. E. Brown, N. Jarmie and G. M. Hale, "Fusion-Energy Reaction 3H(d,a)n at Low Energies", Physical Review C35, 1999-2004 (1987)
H. Brysk, "Fusion Neutron Energies and Spectra", Plasma Physics 15, 611 - 617 (1973)
G. R. Caughlan and W. A. Fowler, "Thermonuclear Reaction Rates V", Atomic Data and Nuclear Data Tables 40, 283 - 334 (1988) and earlier references cited therein.
Hong-Yee Chiu, "Stellar Physics", Volume I, pp. 349 - 363, Blaisdell, Waltham MA, 1968
D. D. Clayton, "Principles of Stellar Evolution and Nucleosynthesis", Chapter 4, pp. 283 - 361, McGraw-Hill, New York, 1968
R. D. Evans, "The Atomic Nucleus", pp. 71 - 74 and pp. 874 - 878, McGraw-Hill, New York, 1955
S. L. Greene, Jr., "Maxwell Averaged Cross Sections for Some Thermonuclear Reactions on Light Isotopes", LLNL report UCRL-70522, May 1967. Preprint for paper in journal Nuclear Physics.
G. Heinrichs, et al. "Analytical Calculation of Source Energy Spectra from Maxwellian Fusion Plasmas of Arbitrary Temperature", Proceedings of the 12th International Conference on Plasma Physics and Controlled Nuclear Fusion Research, Nice, 12 - 19 October 1988, Volume 3, pp. 459 - 468, IAEA-CN-50/G-III-6, Vienna, 1989
R. J. Howerton, "Maxwell-Averaged Reaction Rates 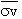 for Selected Reactions Between Ions with Atomic
Mass £ 11", LLNL report UCRL-50400,
Volume 21, Part A, February 1979
for Selected Reactions Between Ions with Atomic
Mass £ 11", LLNL report UCRL-50400,
Volume 21, Part A, February 1979
N. Jarmie, R. E. Brown and R. A. Hardekopf, "Fusion-Energy Reaction 2H(t,a)n from Et = 12.5 to 117 keV", Physical Review C29, 2031 - 2046 (1984)
S. T. Perkins, "TNSPEC, a code to calculate particle spectra and energy deposition terms from thermonuclear reactions", LLNL Nuclear Data Group internal memorandum PD-61, July 1981
S. T. Perkins, "Average energy of interacting particles for thermonuclear reactions", LLNL Nuclear Data Group internal memorandum PD-62, July 1981
S. T. Perkins, "TNSP4DP, a code to calculate particle spectra and energy deposition terms from continuum thermonuclear reactions", LLNL Nuclear Data Group internal memorandum PD-72, July 1982
S. T. Perkins, "Average interaction energy of a suprathermal particle in a Maxwellian plasma", LLNL Nuclear Data Group internal memorandum PD-158, April 1988
S. T. Perkins, "The influence of the center of mass angular distribution on two-body thermonuclear particle spectra", LLNL Monte Carlo Group internal memorandum MC-10, February 1990
S. T. Perkins, "Brief comments on the center of mass system collision cosine for two body reactions on moving targets", LLNL Monte Carlo Group internal memorandum MC-12, January 1991
S. T. Perkins and R. J. Howerton, "Average Energy of Interacting Particles for Thermonuclear Reactions", LLNL report UCRL-87543. Also Nuclear Science and Engineering 82, 388 - 392 (1982)
D. R. Slaughter, "Fusion Reactivities for Several Beam and Target Ion Distributions", LLNL report UCRL-87416, September 1982. Also Journal of Applied Physics 54, 1209 - 1217 (1983)
D. R. Slaughter, "Fusion-Product Spectral Line Width in D-D, D-T and 3He-D Plasmas as an Ion Speed Distribution Diagnostic", LLNL report UCRL-97595, October 1987. Also Review of Scientific Instruments 60, 552 - 61 (1989)
D. R. Slaughter, "Effect of Ion Speed Distribution on the Spectral Shape of the 2.5 MeV Neutron Line Source Produced by DD Fusion", LLNL report UCRL-93895, February 1986. Also Review of Scientific Instruments 57, 1751 - 1753 (1986)
D. R. Slaughter, "Fusion Product Energy Spectra in Beam Heated D-D, D-T and D-3He Plasmas", LLNL report UCRL-93946, March 1986
D. R. Slaughter, "LINE: a code which simulates spectral line shapes for fusion reaction products generated by various speed distributions", LLNL internal report UCID-20374, March 1985
T. L. Talley and G. M. Hale, "Fusion Product Spectra", pp. 299 - 302, proceedings of the 1988 MITO Conference on Nuclear Data for Science and Engineering, JAERI, Japan
S. I. Warshaw, "Burning Issues in Maxwell-Averaged Reaction Rates, Probability Distributions, Data Files and Lookup Codes", LLNL Nuclear Data Group internal memorandum PD-180, Revision I, 1991
R. M. White, LLNL Nuclear Data Group, N Division, private communication (1990)
R. M. White, D. A. Resler and S. I. Warshaw, "Evaluation of Charged Particle Reactions for Fusion Applications", LLNL report UCRL-JC-107158, 7 pp. (May, 1991); Also pp. 834 - 839, proceedings of the International Conference on Nuclear Data For Science and Technology, Julich, Germany, 13 - 17 May 1991.
R. M. White, S. I. Warshaw and D. A. Resler, "Documentation for the files TDF and TDFLIB", LLNL Nuclear Data Group internal memorandum PD-179, December 1990
M. M. R. Williams, "A Generalized Energy Exchange Kernel For Inelastic Neutron Scattering and Thermonuclear Reactions", Journal of Nuclear Energy 25, 489 - 501 (1971)
M. M. R. Williams, "The Particle Spectrum from a D-T Plasma", Nuclear Science and Engineering 73, 219 - 220 (1980)
C. Wong, J. D. Anderson and J. W. McClure, "Neutron Spectrum from the T + T Reaction", Nuclear Physics 71, 106 - 112 (1965)
G. B. Zimmerman, LLNL Defense and Nuclear Technology Directorate, A Division, private communications (1990, 2001).
Appendix A. Example TDF format
-------index/input-------
1 2 d d n he3 ddnevalcs
2 2 d d p t ddpevalcs
3 3 t t n n a tt2nevalcs
4 2 d t n a dtevalcs
5 2 d he3 p a dhe3evalcs
-------------------------
TDFMKRdp version 8a of 11/12/91
(1) ddnevalcs tdfinput tdfout
8A3E911111
(2) amumev fnstnv celer qvalue exval
9.31501E+02 1.37036E+02 2.99792E+10 3.26891E+00 0.00000E-01
(3) amu1 amu2 amu3 amu4 amu5
2.01355E+00 2.01355E+00 1.00866E+00 3.01493E+00 0.00000E-01
(4) iaz1 iaz2 iaz3 iaz4 iaz5 nspec nsigv npart idreac
1002 1002 1 2003 0 13 29 2 1
(5) temp sigvb
extr
1.00000E-04 1.59243E-07 1.43504E-03
1.25000E-04 2.51163E-06 1.67293E-03
1.80000E-04 1.46593E-04 2.15117E-03
2.50000E-04 3.74694E-03 2.70057E-03
3.60000E-04 9.01754E-02 3.48017E-03
5.00000E-04 1.13287E+00 4.37873E-03
7.20000E-04 1.35184E+01 5.65891E-03
1.00000E-03 9.68333E+01 7.14118E-03
1.40000E-03 5.77409E+02 9.07899E-03
2.00000E-03 3.05447E+03 1.17374E-02
2.80000E-03 1.21623E+04 1.49933E-02
4.00000E-03 4.40668E+04 1.94980E-02
5.60000E-03 1.28096E+05 2.50697E-02
8.00000E-03 3.46285E+05 3.28673E-02
1.10000E-02 7.58454E+05 4.20404E-02
1.60000E-02 1.71175E+06 5.64938E-02
2.20000E-02 3.15706E+06 7.30058E-02
3.20000E-02 5.98733E+06 9.93100E-02
4.50000E-02 1.00430E+07 1.32057E-01
6.40000E-02 1.61926E+07 1.77967E-01
9.00000E-02 2.44813E+07 2.38144E-01
1.25000E-01 3.49645E+07 3.15636E-01
1.80000E-01 4.96368E+07 4.31629E-01
2.50000E-01 6.54818E+07 5.72492E-01
3.60000E-01 8.55791E+07 7.84893E-01
4.90000E-01 1.04190E+08 1.02797E+00
6.40000E-01 1.21178E+08 1.30202E+00
8.10000E-01 1.36601E+08 1.60651E+00
1.00000E+00 1.50556E+08 1.94023E+00
(6) spectrum levels, n = 5
6.00000E-01 1.00000E-01 1.00000E-02
1.00000E-03 1.00000E-04
(7) temp particle npoints
area sigvb
1.00000E-04 3 11 1.59173E-07
1.59243E-07
(8) i energy spectrum
integral
1 2.4031589E+00 3.5982959E-03
8.8424660E-06
2 2.4094762E+00 3.5982801E-02
1.0000389E-04
3 2.4169803E+00 3.5982773E-01
1.1942821E-03
4 2.4267775E+00 3.5982847E+00
1.5847336E-02
5 2.4393182E+00 2.1589762E+01
1.5551904E-01
6 2.4505695E+00 3.5982939E+01
5.0117482E-01
7 2.4617310E+00 2.1589762E+01
-1.5660226E-01
8 2.4743616E+00 3.5982850E+00
-1.6027927E-02
9 2.4842743E+00 3.5982782E-01
-1.2123457E-03
10 2.4918941E+00 3.5982817E-02
-1.0181209E-04
11 2.4983269E+00 3.5982980E-03
-9.0249845E-06
(7) temp particle npoints
area sigvb
1.00000E-04 4 11 1.59173E-07
1.59243E-07
(8) i energy spectrum
integral
1 7.7295021E-01 3.5990631E-03
8.6594925E-06
2 7.7915141E-01 3.5990511E-02
9.8207865E-05
3 7.8653932E-01 3.5990483E-01
1.1763575E-03
4 7.9621976E-01 3.5990548E+00
1.5668177E-02
5 8.0866874E-01 2.1594376E+01
1.5444567E-01
6 8.1983442E-01 3.5990628E+01
4.9730239E-01
7 8.3107668E-01 2.1594376E+01
-1.5768205E-01
8 8.4379420E-01 3.5990547E+00
-1.6207574E-02
9 8.5381973E-01 3.5990480E-01
-1.2303020E-03
10 8.6155273E-01 3.5990500E-02
-1.0360734E-04
11 8.6809902E-01 3.5990632E-03
-9.2044831E-06
(7) temp particle npoints
area sigvb
1.00000E-03 3 11 9.67906E+01
9.68333E+01
(8) i energy spectrum
integral
1 2.3063630E+00 1.1358504E-03
8.6424999E-06
2 2.3259784E+00 1.1358504E-02
9.8041043E-05
3 2.3493540E+00 1.1358504E-01
1.1746919E-03
4 2.3799935E+00 1.1358477E+00
1.5651439E-02
5 2.4194130E+00 6.8151017E+00
1.5434509E-01
6 2.4547851E+00 1.1358504E+01
4.9713511E-01
7 2.4904148E+00 6.8151017E+00
-1.5778328E-01
8 2.5307383E+00 1.1358480E+00
-1.6224601E-02
9 2.5625397E+00 1.1358504E-01
-1.2320086E-03
10 2.5870770E+00 1.1358504E-02
-1.0377778E-04
11 2.6078542E+00 1.1358504E-03
-9.2215053E-06
(7) temp particle npoints
area sigvb
1.00000E-03 4 11 9.67908E+01
9.68333E+01
(8) i energy spectrum
integral
1 6.7757772E-01 1.1370148E-03
8.0650292E-06
2 6.9602711E-01 1.1370141E-02
9.2370902E-05
3 7.1823285E-01 1.1370141E-01
1.1180973E-03
4 7.4769523E-01 1.1370124E+00
1.5085648E-02
5 7.8618278E-01 6.8220841E+00
1.5095047E-01
6 8.2126448E-01 1.1370141E+01
4.9147704E-01
7 8.5711205E-01 6.8220841E+00
-1.6117732E-01
8 8.9828560E-01 1.1370123E+00
-1.6790136E-02
9 9.3119974E-01 1.1370141E-01
-1.2885624E-03
10 9.5685723E-01 1.1370141E-02
-1.0943324E-04
11 9.7875840E-01 1.1370151E-03
-9.7870434E-06
Appendix B. Erratum in Williams' original paper.
In the course of developing the equations for the two-body final state particle spectra (viz., dNi/dTi, i = 3, 4) that are presented in Section 5 of this report, we made use of Williams' 1971 paper, and uncovered a nontrivial error in it, which, fortunately, does not affect the final formula for the spectra. It does, however, cause the "general energy exchange kernel" (Williams' equations 11 and 33, which corresponds in part to our function g(v1,v2) as given in Section 5) to have the wrong magnitude, to not be symmetric under exchange of the two final state particle indices 3 and 4, and to be dimensionally incorrect. The multiplicative factor in this kernel is M3(M3/M4)1/2, which does not display the interchange symmetry. The correct factor is (M3M4)3/2. This is the same factor (m3m4)3/2 in the numerator of our normalization function g(v1,v2) as derived in Section 5.
The discrepancy occurs at Williams' improper evaluation of the integral of the momentum d function in his equation 4 to reach his equation 6. Williams treats this three-dimensional integral as if it were one-dimensional. The integral is, in Williams' notation,
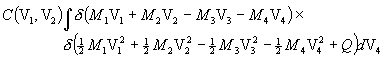 .
.
The correct integration over dV4
that uses up the momentum d
function produces a multiplier of 1/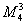 , not the 1/M4
that Williams has. This is because a d function with a vector argument and vector
differential, e.g., d(MV)dV,
is symbolic for the product of d
functions each with a component argument and differential, viz. d(MVx)d(MVy)d(MVz)dVxdVydVz.
Thus the momentum integral over dV4
is actually the product of three "component" integrals, each
of which contributes a factor 1/M4
to the magnitude. The appropriate expressions in Williams' paper from equation
6 on need to be corrected for this multiplicative error.
, not the 1/M4
that Williams has. This is because a d function with a vector argument and vector
differential, e.g., d(MV)dV,
is symbolic for the product of d
functions each with a component argument and differential, viz. d(MVx)d(MVy)d(MVz)dVxdVydVz.
Thus the momentum integral over dV4
is actually the product of three "component" integrals, each
of which contributes a factor 1/M4
to the magnitude. The appropriate expressions in Williams' paper from equation
6 on need to be corrected for this multiplicative error.
Appendix C. Evaluation of a d function integral over finite limits
The derivation of the output particle energy spectrum integral dN3/dT3 requires, at two places, the evaluation of an integral containing a d function over a finite interval. This results in an expression that contains the interval endpoints, and not necessarily just the zero of the d function argument which would be the case if the interval were of infinite extent. The author believes that this aspect of d function integration is not well known, and is providing a discussion of it here as a helpful reference.
A basic d function property is that if the argument of thed function in an integrand is zero in some integration interval, then the integral is equal to the integrand evaluated at that argument zero. Consider the following integral, where the argument of the d function is a linear function in the integration variable:
The d function argument is zero when ax = b, or x = b/a, and we expect that the integral has the value 1/a when b/a falls between x1 and x2, and zero otherwise. To realize this analytically, we make use of the Heaviside step function H(x), which is equal to 1 for positive x and zero for negative x. It can be defined as the integral of the delta function:
Therefore it follows that
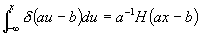 ,
,
and so
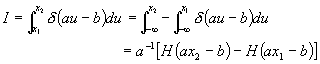
The point of this discussion is that this difference of the step functions is a boxcar function of a and b which defines the interval over which the integral is not zero. If this integral is part of an integrand, and the integrand variable is contained in a and b, then the boxcar function limits defined by ax2 = b and ax1 = b will modify the integrand variable limits if their intervals overlap. We now consider two such cases in the development of the spectrum integral dNi/dTi in Section 5.
The first case occurs during the evaluation of g(v1,v2) and the relevant integral is
which becomes, after integrating over dj3,
where m3 = cosq3, a = p0p3/m4, b = (p02 + p32)/(2m4) + p32/(2m3) - (T1 + T2 + Q), p0 = p1 + p2, and q3 is the angle between p0 and p3. Carrying out the integration over dm3 while using p0 as the angular reference direction results in
What happens now is that the boxcar function in the brackets effectively
changes the integration limits, because the endpoints of the boxcar interval
redefine the limits of integration over dp3. That is, the limits  and
and  are obtained by solving the conditions a ± b = 0 at the zeros of the Heaviside
function arguments. Then the integral easily evaluates to
are obtained by solving the conditions a ± b = 0 at the zeros of the Heaviside
function arguments. Then the integral easily evaluates to
The second case occurs during the evaluation of dN3/dT3, and the relevant integral is
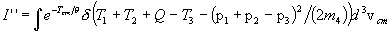
where the symbols have the same meaning as above, and the d function argument is the same, but the integration
variable this time is vcm. Note that 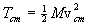 , and that p0 = Mvcm
by definition of vcm, so the directions of p0
and vcm are the same. This means that q3 in
d3p3
is the same as qcm in d3vcm: both are the angle between p3 and p0
= Mvcm. Thus the angular
integration for I˝ is the same as for I´ and proceeds in
the same way.
, and that p0 = Mvcm
by definition of vcm, so the directions of p0
and vcm are the same. This means that q3 in
d3p3
is the same as qcm in d3vcm: both are the angle between p3 and p0
= Mvcm. Thus the angular
integration for I˝ is the same as for I´ and proceeds in
the same way.
After integrating over djcm, the integral I˝ becomes
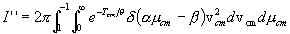
where a and b have the same meaning as before. Carrying out the integration over dmcm with p3 as the angular reference direction gives the result
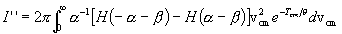
As in the previous case, the boxcar function in the brackets will further
limit the range of integration to lie between the limits 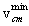 and
and 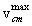 . Those are obtained by solving the conditions
. Those are obtained by solving the conditions
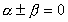 at the zeros of the Heaviside function arguments,
but this time for vcm, or, equivalently, p0/M. When this is done we obtain
at the zeros of the Heaviside function arguments,
but this time for vcm, or, equivalently, p0/M. When this is done we obtain
which is recognized as part of the integrand for dN3/dT3. The exponents in the form shown are discussed at the end of Section 5.
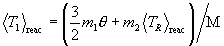
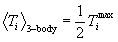
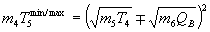 .
.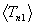
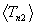
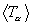
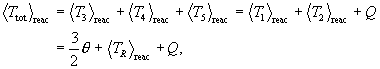
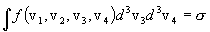 ,
,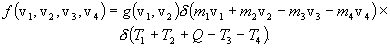
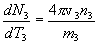 .
.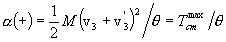 ,
,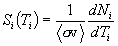
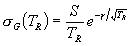 ,
,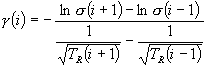 .
.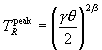 .
.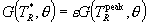
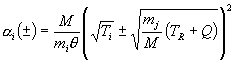 ,
,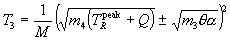 .
.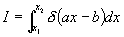 .
.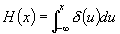 .
.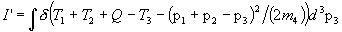
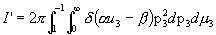
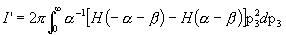 .
.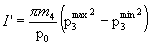 .
.