

Next: Weight Vector Extension
Up: Mathematical Method
Previous: Mathematical Method
For a two-level system in slab geometry that includes collisional pumping between atomic levels,
the radiation transport equation is
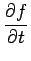 + + 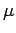 c c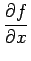 = = 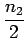 A21 A21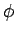 - c - c K12n1-K21n2 K12n1-K21n2 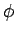 f, f,
|
(1) |
where c is the speed of light, x is the position in the slab, 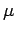 is the direction
cosine of the radiation,
is the direction
cosine of the radiation, 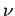 is the frequency of the radiation,
f (
is the frequency of the radiation,
f (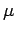 ,
,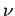 , x, t) is
the photon number density distribution per unit atom density,
n2(x, t) is the upper
level population fraction,
n1(x, t) is the lower level population fraction, A21
is the spontaneous emission rate,
, x, t) is
the photon number density distribution per unit atom density,
n2(x, t) is the upper
level population fraction,
n1(x, t) is the lower level population fraction, A21
is the spontaneous emission rate,
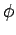 (a,
(a,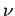 ) is the Voigt line profile normalized to
unit integral [7], and
K12 =
) is the Voigt line profile normalized to
unit integral [7], and
K12 = 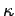 N where
N where 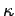 is the lower state
absorption cross section and N is the atom number density. The coefficient K21
is defined by
is the lower state
absorption cross section and N is the atom number density. The coefficient K21
is defined by
K21 = 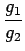 K12, K12,
|
(2) |
where g1 and g2 are the statistical weights for levels 1 and 2, respectively. As in
[3], we consider the problem in the regime of complete redistribution and
no physical scattering of photons.
The equations governing the atomic population fractions n1 and n2 are
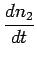 |
= |
C12n1 - C21n2 - A21n2 + c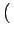 K12n1-K21n2 K12n1-K21n2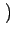 |
|
| |
|
x 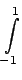 d d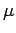 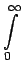 d d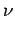 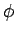 ( (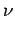 )f ( )f (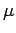 , ,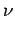 ) ) |
(3) |
and
where C12 and C21 are rate constants for the collisional transitions
1 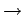 2 and
2
2 and
2 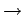 1, respectively. One must also add in appropriate boundary conditions
and initial state to the above equations.
1, respectively. One must also add in appropriate boundary conditions
and initial state to the above equations.
Using (4), equations (1) and (3) may be rewritten as
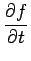 + + 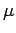 c c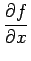 = = 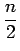 A21 A21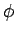 - c - c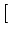 K12- K12-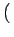 K21+K12 K21+K12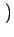 n n![$\displaystyle \left.\vphantom{ {K_{12} - \left( {K_{21} + K_{12} } \right)n}
}\right]$](img23.gif) 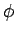 f f
|
(5) |
and
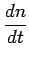 |
= |
C12 -  C12+C21+A21 C12+C21+A21 n + c n + c K12- K12-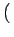 K21+K12 K21+K12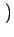 n n![$\displaystyle \left.\vphantom{ {K_{12} - \left( {K_{21} + K_{12} } \right)n}
}\right]$](img23.gif) |
|
| |
|
x 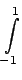 d d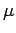 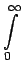 d d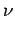 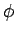  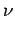  f f 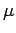 , ,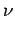 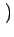 |
(6) |
respectively, where n is the upper level population fraction.
We can generate a finite differencing scheme in time for (6) by using the standard IMC
technique [3]. We integrate (6) from t0 to
t0 + 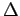 t.
In the spontaneous emission and collision terms, we approximate n(t) by
n(t0 +
t.
In the spontaneous emission and collision terms, we approximate n(t) by
n(t0 + 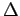 t).
In the absorption term, we substitute n(t0) for n(t) and obtain
t).
In the absorption term, we substitute n(t0) for n(t) and obtain
n(t0 + 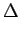 t) t) |
= |
n(t0) + 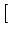 C12- C12-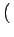 C12+C21+A21 C12+C21+A21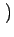 n n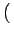 t0+ t0+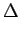 t t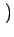 ![$\displaystyle \left.\vphantom{ {C_{12} - \left( {C_{12} + C_{21} + A_{21} } \right)n
\left( {t_0 + \Delta t} \right)} }\right]$](img36.gif) 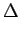 t t |
|
| |
|
+ c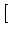 K12- K12-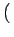 K21+K12 K21+K12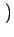 n n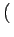 t0 t0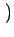 ![$\displaystyle \left.\vphantom{ {K_{12} - \left( {K_{21} + K_{12} } \right)n\left( {t_0 } \right)} }\right]$](img40.gif) |
|
| |
|
x 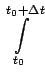 dt dt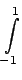 d d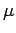 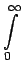 d d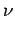 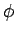  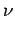  f f 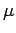 , ,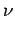 , t , t . . |
(7) |
In the standard IMC technique [3], we substitute
n(t0 + 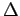 t) from (7) into the spontaneous
emission term of (5) while using n(t0) in the absorption term.
After some algebra, we obtain
t) from (7) into the spontaneous
emission term of (5) while using n(t0) in the absorption term.
After some algebra, we obtain
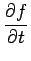 + + 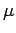 c c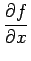 |
= |
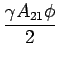  n n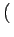 t0 t0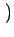 + +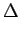 tC12 tC12![$\displaystyle \left.\vphantom{ {n\left( {t_0 } \right) + \Delta tC_{12} }
}\right]$](img46.gif) + + 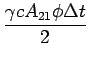 |
|
| |
|
x 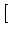 K12- K12-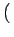 K21+K12 K21+K12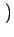 n n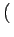 t0 t0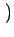 ![$\displaystyle \left.\vphantom{ {K_{12} - \left( {K_{21} + K_{12} } \right)n\left( {t_0 } \right)} }\right]$](img40.gif) 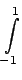 d d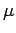 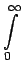 d d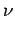 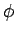  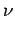 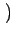 f f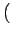 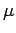 , ,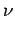  |
|
| |
|
- c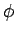  K12- K12- K21+K12 K21+K12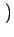 n n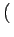 t0 t0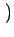 ![$\displaystyle \left.\vphantom{ {K_{12} - \left( {K_{21} + K_{12} } \right)n\left( {t_0 } \right)} }\right]$](img40.gif) f, f, |
(8) |
where 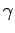 is defined as
is defined as
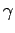 = = 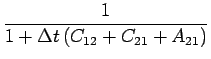 . .
|
(9) |
Equation (8) can be interpreted as a transport equation with a net absorption, 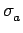 , and effective
scattering,
, and effective
scattering, 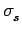 , contribution as given by
, contribution as given by
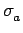 ( (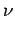 ) = ) = 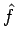 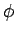 ( (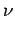 ) ) K12- K12- K21+K12 K21+K12 n(t0) n(t0)![$\displaystyle \left.\vphantom{ {K_{12} - \left( {K_{21} + K_{12} } \right)n(t_0 )} }\right]$](img56.gif)
|
(10) |
and
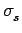 ( (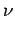 ) = ) = 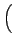 1- 1-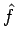 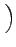 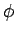 ( (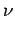 ) ) K12- K12-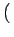 K21+K12 K21+K12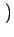 n(t0) n(t0)![$\displaystyle \left.\vphantom{ {K_{12} - \left( {K_{21} + K_{12} } \right)n(t_0 )} }\right]$](img56.gif)
|
(11) |
where the fraction, 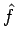 , is given by
, is given by
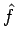 = = 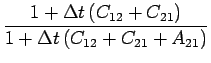 . .
|
(12) |
The fraction, 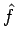 , determines how much effective scattering the problem contains. As
, determines how much effective scattering the problem contains. As 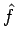 approaches
unity, effective scattering vanishes. The disadvantage of this method is that the effective scattering
term dominates the execution time in optically thick problems, resulting in very long problem runs. Reducing the
effective scattering by making
approaches
unity, effective scattering vanishes. The disadvantage of this method is that the effective scattering
term dominates the execution time in optically thick problems, resulting in very long problem runs. Reducing the
effective scattering by making 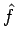 approach 1 requires a smaller time step which also increases execution time
and may reduce accurracy (see Sec. 2.5).
approach 1 requires a smaller time step which also increases execution time
and may reduce accurracy (see Sec. 2.5).
Symbolic Implicit Monte Carlo [4] achieves implicit time integration using a different point of view.
Photons produced by spontaneous emission are given a symbolic weight that remains undetermined until the end of the
time step. The Monte Carlo procedure is the same as for IMC, except there is no effective scattering term. Particle scoring results
in a linear system of equations that are solved for the upper atomic population fraction at the end of a time step.
After spatial discretization (see Sec. 2.3), the upper atomic population is updated with
n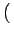 t0+ t0+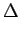 t t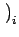 |
= |
n(t0)i + 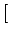 C12- C12-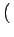 C12+C21+A21 C12+C21+A21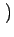 n n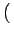 t0+ t0+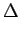 t t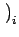 ![$\displaystyle \left.\vphantom{ {C_{12} - \left( {C_{12} + C_{21}
+ A_{21} } \right)n\left( {t_0 + \Delta t} \right)_i } }\right]$](img64.gif) 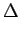 t t |
|
| |
|
+ c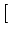 K12- K12-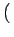 K21+K12 K21+K12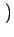 n(t0)i n(t0)i![$\displaystyle \left.\vphantom{ {K_{12} - \left( {K_{21} + K_{12} } \right)n(t_0 )_i } }\right]$](img66.gif) |
|
| |
|
x 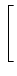 FNi+ FNi+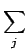 FSijn FSijn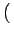 t0+ t0+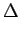 t t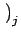 ![$\displaystyle \left.\vphantom{ {FN_i + \sum\limits_j {FS_{ij} n\left( {t_0 + \Delta t} \right)_j } } }\right]$](img70.gif) /Vi. /Vi. |
(13) |
The quantities in the square brackets are short hand for the following integral
In Eq. (13), the term containing FNi is the contribution to the change in upper state population within zone i
from photons that were present at the
beginning of the time step. They have therefore explicit, numerical weights. The term containing
FSijn(t0 + 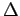 t)j is
a similar contribution coming from bundles with symbolic weights that were born in
zone j during the time step; n(t0)i is the upper level atomic population fraction in zone i at start of
time step;
n(t0 +
t)j is
a similar contribution coming from bundles with symbolic weights that were born in
zone j during the time step; n(t0)i is the upper level atomic population fraction in zone i at start of
time step;
n(t0 + 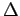 t)i is the unknown upper atomic population fraction in zone i at the end
of the time step; and Vi is the thickness of zone i. For further details, we refer to Ref. [4]. Although the problems we present will involve
small numbers of zones, and as a result the solution of small linear systems using a direct solver,
there is some concern that the size of the linear system to be solved will become intractable using
direct solution methods for problems with larger zone counts. Jacobi iteration [8],
or other more sophisticated techniques, do very well at solving the system of equations given
in (13) by using the values in the previous time step for the initial starting point.
t)i is the unknown upper atomic population fraction in zone i at the end
of the time step; and Vi is the thickness of zone i. For further details, we refer to Ref. [4]. Although the problems we present will involve
small numbers of zones, and as a result the solution of small linear systems using a direct solver,
there is some concern that the size of the linear system to be solved will become intractable using
direct solution methods for problems with larger zone counts. Jacobi iteration [8],
or other more sophisticated techniques, do very well at solving the system of equations given
in (13) by using the values in the previous time step for the initial starting point.


Next: Weight Vector Extension Up: Mathematical Method Previous: Mathematical Method
![]() t.
In the spontaneous emission and collision terms, we approximate n(t) by
n(t0 +
t.
In the spontaneous emission and collision terms, we approximate n(t) by
n(t0 + ![]() t).
In the absorption term, we substitute n(t0) for n(t) and obtain
t).
In the absorption term, we substitute n(t0) for n(t) and obtain
![]() t) from (7) into the spontaneous
emission term of (5) while using n(t0) in the absorption term.
After some algebra, we obtain
t) from (7) into the spontaneous
emission term of (5) while using n(t0) in the absorption term.
After some algebra, we obtain
![]() , and effective
scattering,
, and effective
scattering, ![]() , contribution as given by
, contribution as given by
![]() , determines how much effective scattering the problem contains. As
, determines how much effective scattering the problem contains. As ![]() approaches
unity, effective scattering vanishes. The disadvantage of this method is that the effective scattering
term dominates the execution time in optically thick problems, resulting in very long problem runs. Reducing the
effective scattering by making
approaches
unity, effective scattering vanishes. The disadvantage of this method is that the effective scattering
term dominates the execution time in optically thick problems, resulting in very long problem runs. Reducing the
effective scattering by making ![]() approach 1 requires a smaller time step which also increases execution time
and may reduce accurracy (see Sec. 2.5).
approach 1 requires a smaller time step which also increases execution time
and may reduce accurracy (see Sec. 2.5).