Equiprobable bins

For pairs of values (x, P(x)) with P a probability density, the routine eqpb uses linear interpolation to compute equi_dist, an equidistributed probability density. There are two basic applications of this routine: angular distributions ( $\tt I\_number$ = 1) data and distributions of energy carried off by secondary particles ( $\tt I\_number$ = 4 data). But there is also the $\tt I\_number$ = 3 data for correlated distributions of angle and energy. We begin with a description of the general method and discuss later the special provisions made for the correlated distributions for $\tt I\_number$ = 3.

The method used is as follows. Suppose that we want $\tt nbins$ bins, each with probability 1/$\tt nbins$, with the bottom of the lowest bin and the top of the highest bin fixed by the lowest and highest input values of x. The equidistributed interior bin boundaries are located at the x-values for which the accumulated probabilities are k/$\tt nbins$ for k = 1, 2, ..., $\tt nbins$ - 1. The geometry of the problem is that we want the set of x points which give equal area under the graph of P. From a mathematical point of view, what we want is the points $\xi_{k}^{}$ (for k = 0, 1, ..., nbins) such that $\xi_{0}^{}$ is the first library x-value and

$$\int_{{\xi_0}}^{{\xi_k}}$$P(x) dx = $${k \over {\tt nbins}}$$.

But P is piecewise linear, so this condition requires us to add up areas of trapezoids.

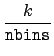Suppose that we seek the k-th equidistribution point, $\xi_{k}^{}$. We start by adding the areas of the trapezoids given by the library (x, P(x)) data, and we eventually find the first time that the accumulated sum exceeds the desired area k/$\tt nbins$. This brackets $\xi_{k}^{}$ between two of the library x-values, and P is linear on this interval. The integral of P is therefore quadratic on the interval, and the determination of $\xi_{k}^{}$ requires the solution of a quadratic equation. Only one root of the quadratic makes physical sense, and the algorithm takes advantage of this fact.

The extraneous root is easily understood by looking at the Fig. 1. In that figure suppose that B is the equidistribution point we are looking for, and suppose we know that B lies between the two library x-values A and C. The library probability distribution is a broken-line function P(x) which is equal to a linear function L(x) on the interval A$\le$x$\le$C. In the figure we have extrapolated L(x) as a dashed line out to D. Note that

$$\int_{A}^{B}$$P(x) dx = $$\int_{A}^{B}$$L(x) dx,

and this integral is easy to evaluate because we have a formula for L(x). But because of the congruent triangles BRQ and DRS, it is clear that

$$\int_{A}^{B}$$L(x) dx = $$\int_{A}^{D}$$L(x) dx.

Therefore, the quadratic equation for the equidistribution point has two roots, B and D, but the root D is physically impossible.

Figure 4.1: Only one root is physical.