


Up: Code details for mcfgen
Previous: Equiprobable bins
Contents
The algorithm to produce equidistributed correlated angle-energy bins
from
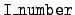 = 3 data is implemented by the routine iequ3. The data for both the angle-energy probability densities
(
= 3 data is implemented by the routine iequ3. The data for both the angle-energy probability densities
(
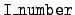 = 3) and for the angular probability densities
(
= 3) and for the angular probability densities
(
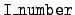 = 1) must be present. Furthermore, the lists of
incident energies at which the
= 1) must be present. Furthermore, the lists of
incident energies at which the
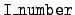 = 3 and
= 3 and
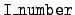 = 1 probability densities are given must be identical.
= 1 probability densities are given must be identical.
The computation of equiprobable angle-energy is done in three
steps. First, the
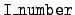 = 1 data is used to make an
equidistribution of the cosines using the method described above. For
each of these equidistributed cosines we need to create
equidistributed secondary energy bins. So, the second step is the
creation of secondary energy distributions at these new cosines. The
third step is the equidistribution of these energies. The only new
step here is the second step, that of making an energy distribution at
one of the edges of an equiprobable cosine bin. Its details are as
follows.
= 1 data is used to make an
equidistribution of the cosines using the method described above. For
each of these equidistributed cosines we need to create
equidistributed secondary energy bins. So, the second step is the
creation of secondary energy distributions at these new cosines. The
third step is the equidistribution of these energies. The only new
step here is the second step, that of making an energy distribution at
one of the edges of an equiprobable cosine bin. Its details are as
follows.
Consider one of the equidistributed cosines. We bracket it between
two
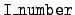 = 3 (or equivalently,
= 3 (or equivalently,
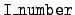 = 1)
cosines from the `library' file. We want to use the (energy,
probability density) data from these bracketing cosines to produce
(energy, probability density) pairs for the new cosine. This is
illustrated in the Fig. 2, which has secondary energy increasing to
the right and cosine increasing upward. Suppose that the new cosine
Cnew lies between the library cosines C0 and C1. We
want probability densities for
Cnew, given probability
densities at one set of energies for C0 (denoted by dots) and at
another set of energies for C1 (denoted by crosses). The algorithm
is based on multiple linear interpolation as follows.
= 1)
cosines from the `library' file. We want to use the (energy,
probability density) data from these bracketing cosines to produce
(energy, probability density) pairs for the new cosine. This is
illustrated in the Fig. 2, which has secondary energy increasing to
the right and cosine increasing upward. Suppose that the new cosine
Cnew lies between the library cosines C0 and C1. We
want probability densities for
Cnew, given probability
densities at one set of energies for C0 (denoted by dots) and at
another set of energies for C1 (denoted by crosses). The algorithm
is based on multiple linear interpolation as follows.
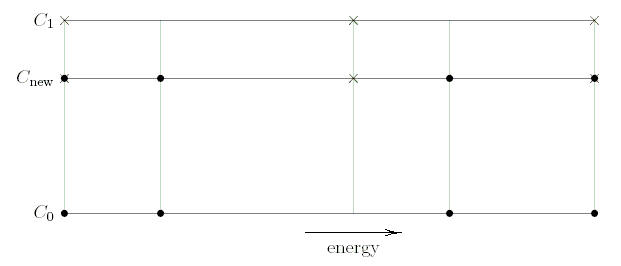
Figure 4.2: Double interpolation of probability
density.
- 1.
- We start by translating and scaling the secondary energy
ranges for the cosines C0 and C1 to the interval
0
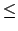 E
E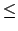 1, and we scale the probability densities correspondingly.
The figure shows the situation after this scaling. There are
several reasons for starting with this scaling. For one thing, it
ensures proper linear dependence on incident energy for the
minimum and maximum energy of the secondary particle. For
another, it leads to more accurate interpolation of such physical
features as resonance peaks. Finally, it makes the interpolation
process clearer.
1, and we scale the probability densities correspondingly.
The figure shows the situation after this scaling. There are
several reasons for starting with this scaling. For one thing, it
ensures proper linear dependence on incident energy for the
minimum and maximum energy of the secondary particle. For
another, it leads to more accurate interpolation of such physical
features as resonance peaks. Finally, it makes the interpolation
process clearer.
- 2.
- We merge these scaled energy lists to produce a master
secondary energy list, denoted by the vertical lines in the figure.
- 3.
- For each library cosine C0 and C1 we interpolate in
energy to get probability densities at the full merged list of
secondary energies. This is interpolation horizontally along the
top and bottom of the rectangle in Fig. 2.
- 4.
- Then at each secondary energy we interpolate vertically in
the figure, to get the probability densities at the equiprobable
cosine
Cnew.
- 5.
- Now that we have probability densities, we use the method
described in the previous section to get equiprobable secondary
energy bins at
Cnew, but these are still scaled to
0
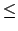 E
E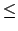 1.
1.
- 6.
- Finally, we undo the scaling by mapping from
0
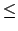 E
E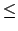 1 to the physical energy interval.
1 to the physical energy interval.
- 1.
- D. E. Cullen,
``TART95: A coupled neutron-photon Monte Carlo transport code'',
Report UCRL-MA-121319, Lawrence Livermore National Laboratory,
July 1995.
- 2.
- R. J. Howerton, R. E. Dye, P. C. Giles,
J. R. Kimlinger, S. T. Perkins, and E. F. Plechaty, ``OMEGA: a
Cray 1 executive code for LLNL nuclear data libraries'', Report
UCRL-50400, Vol. 25, Lawrence Livermore National Laboratory,
August 1983.
- 3.
- R. J. Howerton, R. E. Dye, and S. T. Perkins,
``Evaluated nuclear data libraries'', Report UCRL-50400, Vol. 4,
Rev. 1, Lawrence Livermore National Laboratory, October 1981.
- 4.
- S. T. Perkins, ``Specification of the all-particle
Monte Carlo data files, MCFYi'', Draft Report, Lawrence Livermore
National Laboratory, July 1994.
- 5.
- J. A. Rathkopf, ``Format of binary ENDL-type
libraries'', Report #PD-166, Lawrence Livermore National
Laboratory, 17 October 1988.
Work performed under the auspices of the U. S. Department of
Energy by Lawrence Livermore National Laboratory under Contract
W-7405-Eng-48.



Up: Code details for mcfgen Previous: Equiprobable bins Contents
![]() = 3 data is implemented by the routine iequ3. The data for both the angle-energy probability densities
(
= 3 data is implemented by the routine iequ3. The data for both the angle-energy probability densities
(
![]() = 3) and for the angular probability densities
(
= 3) and for the angular probability densities
(
![]() = 1) must be present. Furthermore, the lists of
incident energies at which the
= 1) must be present. Furthermore, the lists of
incident energies at which the
![]() = 3 and
= 3 and
![]() = 1 probability densities are given must be identical.
= 1 probability densities are given must be identical.
![]() = 1 data is used to make an
equidistribution of the cosines using the method described above. For
each of these equidistributed cosines we need to create
equidistributed secondary energy bins. So, the second step is the
creation of secondary energy distributions at these new cosines. The
third step is the equidistribution of these energies. The only new
step here is the second step, that of making an energy distribution at
one of the edges of an equiprobable cosine bin. Its details are as
follows.
= 1 data is used to make an
equidistribution of the cosines using the method described above. For
each of these equidistributed cosines we need to create
equidistributed secondary energy bins. So, the second step is the
creation of secondary energy distributions at these new cosines. The
third step is the equidistribution of these energies. The only new
step here is the second step, that of making an energy distribution at
one of the edges of an equiprobable cosine bin. Its details are as
follows.
![]() = 3 (or equivalently,
= 3 (or equivalently,
![]() = 1)
cosines from the `library' file. We want to use the (energy,
probability density) data from these bracketing cosines to produce
(energy, probability density) pairs for the new cosine. This is
illustrated in the Fig. 2, which has secondary energy increasing to
the right and cosine increasing upward. Suppose that the new cosine
Cnew lies between the library cosines C0 and C1. We
want probability densities for
Cnew, given probability
densities at one set of energies for C0 (denoted by dots) and at
another set of energies for C1 (denoted by crosses). The algorithm
is based on multiple linear interpolation as follows.
= 1)
cosines from the `library' file. We want to use the (energy,
probability density) data from these bracketing cosines to produce
(energy, probability density) pairs for the new cosine. This is
illustrated in the Fig. 2, which has secondary energy increasing to
the right and cosine increasing upward. Suppose that the new cosine
Cnew lies between the library cosines C0 and C1. We
want probability densities for
Cnew, given probability
densities at one set of energies for C0 (denoted by dots) and at
another set of energies for C1 (denoted by crosses). The algorithm
is based on multiple linear interpolation as follows.
