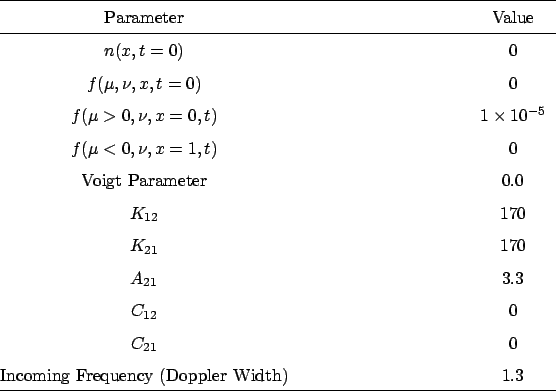 |
Our second problem is the line transport version of a slab with surface heating. Low intensity radiation impinges on the left surface of an optically thick slab perpendicularly. The incoming beam is monochromatic in the wing of the line. As the beam penetrates the slab, photons are absorbed and reemitted with a spectrum given by the line profile. The slab is initially cold and has an initial optical depth of 100 at line center. The problem parameters are given in Table 2.
The incoming radiation heats the slab, first heating the surface and then causing it to emit radiation with a profile characteristic of the trapping problem presented in Sec. 3.1. The excitation then traverses the slab and transmission eventually occurs out the far side. This form of heating is interesting in that it clearly shows how IMC and SIMC can make systematic errors. The data in Figs. 7 and 8 is for time = 200, achieving steady-state at the surface and extending to the middle of the slab, but is just short of steady-state for the transmitted radiation due to the long time to penetrate the slab. We vary the time step size and the number of zones, in order to examine the effect on the IMC and SIMC methods.
In Fig. 7, the upper level atomic population versus position, at time 200, for the first 20% of the slab is shown. The "Base IMC" and "Base SIMC" curves are shown for 21 equally spaced zones, and a time step size of 5. Also shown is the result for the IMC algorithm, with the time step size reduced by a factor of 256, and the result for the SIMC algorithm, with the zone size reduced by a factor of 10. This refined zoning for the SIMC algorithm provides the correct solution for the problem, with the 21 zone IMC solution being close to correct in the sense of the average of the correct solution over the coarser zoning. The results for SIMC with 21 zones suffer from photon teleportation problems, as discussed in Sec. 2.5. The IMC algorithm is less sensitive to photon teleportation, as long as one does not refine the time step. When the time step for IMC is reduced by a factor of 256, it also suffers teleportation error, falling into agreement with SIMC for the 21 zone case. The IMC does well for a coarse zone and time step choice (apart from increased noise), but the solution moves in the wrong direction when the time step size is reduced.
In Fig. 8, we show the flux leaving the right hand side of the slab at time 200. All of the methods, and choices of zoning and time step size, neglecting noise, agree pretty well where significant energy is transported far from line center. Again, photon teleportation becomes a problem near line center if the time step for IMC is refined, or large zone sizes are used for SIMC. Note the very significant advantage for SIMC with weight vectors in the region where significant energy is transported.
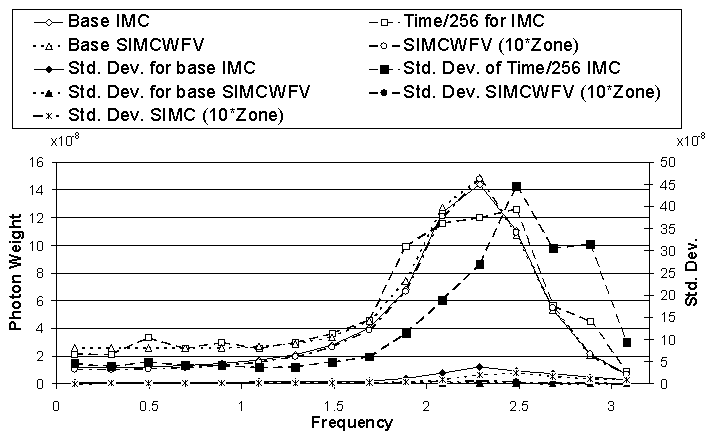
Figure 8:
Photon Frequency Distribution Leaving the Right Side of the Slab for Surface
Heating Example
The effects of photon teleportation error become clear when we examine the time dependent heating of a region near the surface of the slab (the region occupied by the first zone for the case of 21 equally spaced zones and average of the corresponding zones in the case of 210 zones) and the time dependent heating of a similar region in the middle of the slab. Again, IMC and SIMC with zone refinement give correct solutions. In Fig. 9, we show the surface heating as a function of time. In this case, teleportation error results in slower heating and an overall colder region. In Fig. 10, we show the heating in the middle of the slab as a function of time. Accumulated photon teleportation error is overheating this region. This is consistent with the view that photon teleportation error moves energy through the material too quickly.
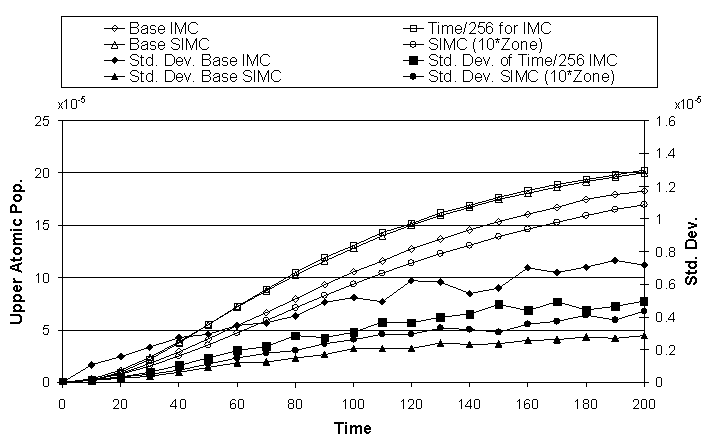
Figure 10:
Mid-slab Heating as a Function of Time for Surface Heating Problem
Overall, this example demonstrates that IMC is much more forgiving than SIMC, with respect to bad zoning. One must be careful, however, in becoming too reliant on this feature of IMC. IMC will suffer from photon teleportation error if the time step is refined, and the user may think that the solution is getting better rather than worse. Therefore, we have concluded that the convergence characteristics of IMC, in response to time step and zone refinement, are very poor and it is hard to know that one has a correct solution. SIMC, on the other hand, demonstrates rapid convergence in response to time step and zone refinement.