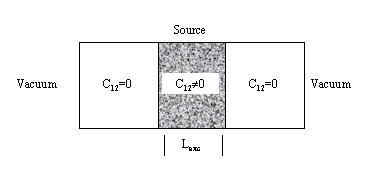
Figure 11: Milne's Problem Layout
In our last test problem, we consider a localized source in the middle of the slab and an opacity that is independent of frequency. This approximation for the opacity, known as the grey approximation or Milne's problem [7], offers an analytical solution that can be used to check the accuracy of the numerical results.

Figure 11:
Milne's Problem Layout
We simulate a grey slab by defining only one energy group of width ![]()
![]() . The physical configuration of this problem can be seen in Fig.
11. We define a central zone to provide a source
of collisionally pumped photons of width Lexc. In this central
zone, C12 is to set a small value consistent with the approximations
required for an analytical solution. The problem is set up with 21 equally spaced
zones and the physical parameters specified in Table 3.
. The physical configuration of this problem can be seen in Fig.
11. We define a central zone to provide a source
of collisionally pumped photons of width Lexc. In this central
zone, C12 is to set a small value consistent with the approximations
required for an analytical solution. The problem is set up with 21 equally spaced
zones and the physical parameters specified in Table 3.
The analytical solution is provided in Appendix A. We cannot easily solve for n close to the pumped region or near the edge of the slab since the boundary layers add additional complexity. However, the slope of n far from the boundaries may be obtained analytically.
The predicted slope of n versus position, equation (A-7)
from the appendix, is
-1.7 x 10-4. The results of IMC and SIMC have been plotted in Fig.
12. IMC and SIMC produce slopes of
-1.7 x 10-4 and
-1.3 x 10-4, respectively. Although SIMC has a lower noise figure than IMC, as seen in this
graph, it produces the wrong slope. The directional dependence of photons, ![]() , as defined in
equation (B-1) was found experimentally to be about 1.6.
, as defined in
equation (B-1) was found experimentally to be about 1.6.
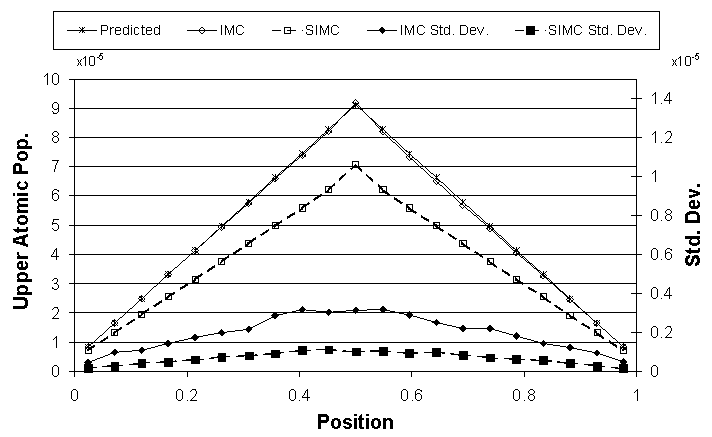
Figure 12: Results
for Milne's Problem
This error for SIMC is due to the teleportation problem discussed in Sec. 2.5. When we refine the zoning by a factor of ten, which reduces the optical depth per zone, SIMC and IMC both agree with the predicted slope, -1.7 x 10-4. Attempts to use geometric zoning schemes, with thick zones in the middle of the uniform regions on the left and right sides of this problem, suffer from the photon teleportation problems described previously.
Equation (B-5) from the appendix, displayed below, shows how teleportation error affects the predicted slopes for this problem.
![$\displaystyle {\frac{{{3F\left[ {K_{12}
- \left( {K_{21} + K_{12} } \right)\bar n} \right]^2 }}}{{{A_{21} \Delta \nu ^2 }}}}$](img92.gif)
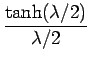 .
.
In this example problem for SIMC, ![]() is 2.16 (assuming the value of
is 2.16 (assuming the value of ![]() to be 1.6) while a tenfold
increase in zoning leads to a
to be 1.6) while a tenfold
increase in zoning leads to a ![]() of 0.216. Since in the derivation of equation (B-5) we assumed
of 0.216. Since in the derivation of equation (B-5) we assumed ![]() was much less than
1, we cannot use it to double check the computed slope of the example problem. However, we can see that a
was much less than
1, we cannot use it to double check the computed slope of the example problem. However, we can see that a ![]() of 0.216 yields a 0.4% error. While not derived for the collisionally pumped trap problem, it does reinforce
the observation that you need finer zoning in places of large slope while zones with little to no slope
do not need as much refinement.
of 0.216 yields a 0.4% error. While not derived for the collisionally pumped trap problem, it does reinforce
the observation that you need finer zoning in places of large slope while zones with little to no slope
do not need as much refinement.
In the IMC method, the effective scattering reduces the absorption and this must be taken into account. The resulting
equation is very similar to (B-5) with a minor change. Since the absorption cross section
is
![]()
![]() as given in equation (10), the absorption per zone is reduced by a factor
of
as given in equation (10), the absorption per zone is reduced by a factor
of ![]() . This results in a prediction for the slope for IMC as
. This results in a prediction for the slope for IMC as
From this expression, we can see how IMC's effective scattering dampens the teleportation error. As ![]() approaches 1
(corresponding to smaller time steps), the scattering contribution disappears and this equation approaches
equation (B-5) and behaves as SIMC. As
approaches 1
(corresponding to smaller time steps), the scattering contribution disappears and this equation approaches
equation (B-5) and behaves as SIMC. As ![]() decreases, the multiplicative term from above
contributes less and less to the behavior of the slope. The limiting value of
decreases, the multiplicative term from above
contributes less and less to the behavior of the slope. The limiting value of ![]() is
is
![]() C12+C21
C12+C21![]() /
/![]() C12+C21+A21
C12+C21+A21![]() which represents the most that
the teleportation error may be dampened.
which represents the most that
the teleportation error may be dampened.