


Next: Remark
Up: What mcfgen does for
Previous: Initial processing for each
Contents
Loop over the reactions
We have mentioned that for each target the routine trgdat
transfers the corresponding data from the `library' file to the
scratch file `endata'. The code mcfgen reads data from
the file `endata', processes it, and prints the results to the
output file `mcf.asc'. For a given reaction the order of the
processing is according to the data type as given by the identifier
I_number. For the different values of I_number the
various types of data are as follows. Note that no single reaction
has all of this data.
-
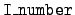 = 0:
= 0:
- The original data in the `library' file is an array of pairs (incident energy, reaction
cross section). The subroutine iequ0 computes and prints
flux-weighted averages over the groups g,
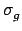
=
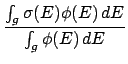
.
The integration is done by the trapezoid rule. The flux 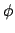 is
usually constant over each group. The code also calculates and
prints out the total available energy.
is
usually constant over each group. The code also calculates and
prints out the total available energy.
-
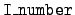 = 1:
= 1:
- The data consists of pairs (energy
deposited to secondary particle, probability density) for a
sequence of incident energies and cosines of the collision angle.
Depending on the kinematics type, this data may be in the
laboratory or the center-of-mass system. The subroutine iequ1 computes boundaries for equiprobable cosine bins, and it
prints them. See Section 4.2.
-
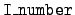 = 3:
= 3:
- The data consists of pairs (energy of
the secondary particle, probability density) for a sequence of
incident energies and cosines of the collision angle. This data
is in the center-of-mass system. The subroutine iequ3
computes boundaries for joint equiprobable cosine bins and energy
bins, and it prints them. This type of data is given only for the
9Be
(n, 2n
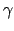 )2
)2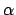 reaction and for the Production
Cross Section Library. Note that this block of data is not
self-sufficient--the angular-distribution data (
reaction and for the Production
Cross Section Library. Note that this block of data is not
self-sufficient--the angular-distribution data (
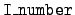 = 1) must be present and must be consistent. The
= 1) must be present and must be consistent. The
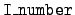 = 1 and 3 data together provide joint (energy, angle)
probability distributions.
= 1 and 3 data together provide joint (energy, angle)
probability distributions.
-
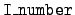 = 4:
= 4:
- The data consists of pairs (energy of
secondary, probability density) for a sequence of incident
energies. This data is in the laboratory system. The subroutine
iequ4 computes equiprobable energy bins and writes them
(along with the incident energies) to the `mcf.asc' output
file.
-
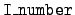 = 7 or 9:
= 7 or 9:
- The cases of data type 7
and 9 are treated together by the subroutine iequ7or9. In
both cases the data is an array of pairs (incident energy,
multiplicity). For data type 7 the particles are fission
neutrons, and for type 9 the data gives the multiplicity of
emitted photons. The fission neutrons may be prompt or delayed.
The code computes average multiplicities over the energy groups g,
weighted by the flux and reaction cross section,
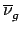
=
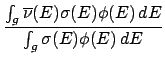
,
It then prints the results to the `mcf.asc' file.
-
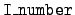 = 10:
= 10:
- The data in the `library' file
consists of pairs (energy, energy deposition to secondary
particle). This data may be in the center-of-mass system or the
laboratory system, depending on the kinematics type of the
reaction. The subroutine iequ10 computes the average energy
deposited in each energy group g,
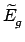
=
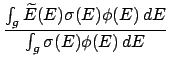
,
and it prints the results to the `mcf.asc' file.
-
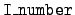 = 12:
= 12:
- This flag is used only for making
Production Cross Section files. When
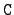 = 5 the `library' file contains pairs (E, Q), where E is the incident
energy and Q the energy available from non-elastic reactions.
The code computes and prints the group averages
= 5 the `library' file contains pairs (E, Q), where E is the incident
energy and Q the energy available from non-elastic reactions.
The code computes and prints the group averages
Qg =
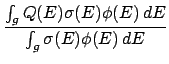
.
This processing is done inside the subroutine iequ0.



Next: Remark Up: What mcfgen does for Previous: Initial processing for each Contents
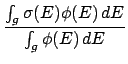 .
.
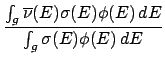 ,
,
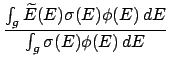 ,
,
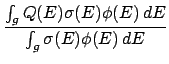 .
.
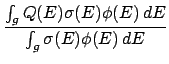 .
.
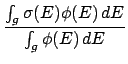 .
.
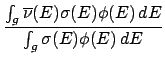 ,
,
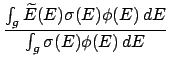 ,
,
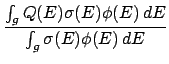 .
.