Qlg = 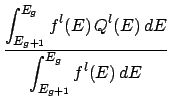 . .
|
(1) |
Data that is only a function of incident particle energy is grouped by performing a Legendre-order-flux weighted averaging of the data between group boundaries. That is, for the lth Legendre order Ql of a quantity Q(E) and the lth Legendre order flux fl(E), the value of Ql for group g, Qlg, is calculated as,
Only the transport correcting cross-sections and the interaction transfer matrix have l > 0 Legendre orders. All other quantities have only the isotropic l = 0 Legendre order; in which case the l-order label is dropped (e.g.,
| = | 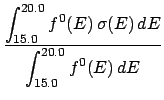 |
(2) | |
| = | 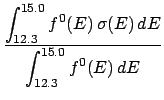 |
(3) | |
| = | 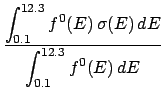 . . |
(4) |
Often the data in a ndfy![]() file are stored with more energy resolution than a problem requires. In this
case, the user can request, by calling ndfgroup, that the ndf
access routines return the data grouped to a smaller energy group.
This smaller energy group must be a subset of the energy group used to generate the data
in the ndfy
file are stored with more energy resolution than a problem requires. In this
case, the user can request, by calling ndfgroup, that the ndf
access routines return the data grouped to a smaller energy group.
This smaller energy group must be a subset of the energy group used to generate the data
in the ndfy![]() file. (A subset energy group contains only boundaries of the superset group).
The example above has six 1-group subsets (20.0, 15.0), (20.0, 12.3), (20.0, 0.1), (15.0, 12.3),
(15.0, 0.1), and (12.3, 0.1), four 2-group subsets (20.0, 15.0, 12.3), (20.0, 15.0, 0.1), (20.0, 12.3, 0.1) and
(15.0, 12.3 0.1) and itself as a 3-group subset.
file. (A subset energy group contains only boundaries of the superset group).
The example above has six 1-group subsets (20.0, 15.0), (20.0, 12.3), (20.0, 0.1), (15.0, 12.3),
(15.0, 0.1), and (12.3, 0.1), four 2-group subsets (20.0, 15.0, 12.3), (20.0, 15.0, 0.1), (20.0, 12.3, 0.1) and
(15.0, 12.3 0.1) and itself as a 3-group subset.
Data mapped to a subset group is referred to as
collapsed data in this document and the act of mapping the data is called collapsing. To receive collapsed data
one must first call the ndf routine ndfgroup (or ndfcgroup).
The first two arguments of ndfgroup are the new group
boundaries and the number of new groups (labeled ncg is this document).
The third argument of this routine is a flux id. The bdfls file is scanned
for the requested flux. This flux ![]() is then grouped onto the old groups and the data is collapsed using this flux
as a weight for the old group data.
The flux is calculated as,
is then grouped onto the old groups and the data is collapsed using this flux
as a weight for the old group data.
The flux is calculated as,
Collapsing a quantity Qlg is calculated as,
In the above example, collapsing the cross-section to the 2-group (20.0, 15.0, 0.1) yields,| = | (10) | ||
| = | 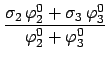 . . |
(11) |
| = | 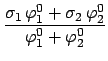 . . |
(12) |
The speed (and flux as given in Eq. 7) is collapsed differently, so as to be consistent with its previous groupings. Speed is collapsed as,