


Next: Types of data in
Up: Energy grouping and data
Previous: Grouping and collapsing data
Contents
Grouping and collapsing data dependent on incident and outgoing energies
This section discusses grouping and collapsing of transfer and fission matrix data.
These data are dependent on both incident and outgoing particles' energies.
Grouping and collapsing of transfer matrix data are more complicated than is presented here, since either
particle number, energy, or number-and-energy of the outgoing particles is conserved during the grouping and collapsing.
In this section only particle conserving grouping and collapsing will be discussed.
A full discussion of grouping and collapsing of the transfer matrix data can be found in Chapter
VI and pages VII-19 to VII-23 of reference [1] and in reference [2].
If M(E, E') is a quantity that is dependent on incident E and outgoing E' energies and
fl(E) is the l-order Legendre flux then
the l-order Legendre particle-conserving grouped matrix Mg, hl is calculated as,
Mg, hl = 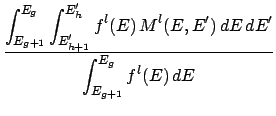 . .
|
(14) |
Collapsing this data to new incident and outgoing particle groups, label as g' and h',
is calculated as,
Mg', h'l = 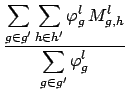 . .
|
(15) |
Here g 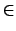 g' means to sum over all g for which the boundaries of g fall inclusively between
the boundaries of g' and h
g' means to sum over all g for which the boundaries of g fall inclusively between
the boundaries of g' and h 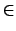 h' means to sum over all h for which the boundaries of h fall inclusively between
the boundaries of h' except that the end points of h' are extended to include the
end points of h so as to conserve outgoing particle number. For example,
collapsing the outgoing particle's group from (20.0, 15.0, 12.3, 0.1) to (20.0, 15.0, 12.3) will result in the
outgoing particle's collapse group being (20.0, 15.0, 0.1) when collapsing.
The incident particle's collapse group is set by calling ndfgroup or ndfcgroup. For the interaction
transfer matrix data and the fission transfer matrix data
the outgoing particle's collapse group is also that set by calling ndfgroup
or ndfcgroup.
For transfer matrix data for yi
h' means to sum over all h for which the boundaries of h fall inclusively between
the boundaries of h' except that the end points of h' are extended to include the
end points of h so as to conserve outgoing particle number. For example,
collapsing the outgoing particle's group from (20.0, 15.0, 12.3, 0.1) to (20.0, 15.0, 12.3) will result in the
outgoing particle's collapse group being (20.0, 15.0, 0.1) when collapsing.
The incident particle's collapse group is set by calling ndfgroup or ndfcgroup. For the interaction
transfer matrix data and the fission transfer matrix data
the outgoing particle's collapse group is also that set by calling ndfgroup
or ndfcgroup.
For transfer matrix data for yi yo the outgoing particle's collapse group is specified through arguments
to the routines dfpmat and ndfcpmat.
yo the outgoing particle's collapse group is specified through arguments
to the routines dfpmat and ndfcpmat.



Next: Types of data in Up: Energy grouping and data Previous: Grouping and collapsing data Contents
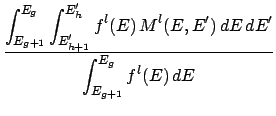 .
.